题目内容
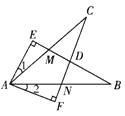
【题目】(10分)如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F。

(1)求证:△ABE≌△CAD;(2)求∠BFD的度数。
【答案】(1)见解析;(2)60°
【解析】
试题分析:(1)根据等边三角形的性质可知∠BAC=∠C=60°,AB=CA,结合AE=CD,可证明△ABE≌△CAD,从而证得结论;
(2)根据∠BFD=∠ABE+∠BAD,∠ABE=∠CAD,可知∠BFD=∠CAD+∠BAD=∠BAC=60°.
试题解析:(1)证明:∵△ABC为等边三角形,
∴∠BAC=∠C=60°,AB=CA,
即∠BAE=∠C=60°,
在△ABE和△CAD中, ,
,
∴△ABE≌△CAD(SAS)。
(2)解:∵∠BFD=∠ABE+∠BAD,
又∵△ABE≌△CAD,
∴∠ABE=∠CAD.
∴∠BFD=∠CAD+∠BAD=∠BAC=60°.

练习册系列答案
相关题目
【题目】我市某校准备组织学生及学生家长坐高铁到杭州进行社会实践,为了便于管理.所有人员必须乘坐在同一列高铁上.根据报名人数,若都买一等座单程火车票需6560元,若都买二等座单程火车票,则需3120元(学生票二等座打7.5折,一等座不打折).已知学生家长与教师的人数之比为3:1,余姚北站到杭州东站的火车票价格如表所示:
运行区间 | 票价 | ||
上车站 | 下车站 | 一等座 | 二等座 |
余姚北 | 杭州东 | 82(元) | 48(元) |
(1)参加社会实践的老师、家长与学生各有多少人?
(2)由于各种原因,二等座火车票单程只能买m张(m小于参加社会实践的人数),其余的须买一等座火车票,在保证每位参与人员都有座位坐的前提下,请你设计最经济的购票方案,并写出购买火车票的总费用(单程)y(元)(用含m的代数式表示).