Question

【题目】如图，已知抛物线y=ax2+bx+c经过点A（﹣3，0），B（9，0）和C（0，4）．CD垂直于y轴，交抛物线于点D，DE垂直与x轴，垂足为E，l是抛物线的对称轴，点F是抛物线的顶点．

（1）求出二次函数的表达式以及点D的坐标；
（2）若Rt△AOC沿x轴向右平移到其直角边OC与对称轴l重合，再沿对称轴l向上平移到点C与点F重合，得到Rt△A1O1F，求此时Rt△A1O1F与矩形OCDE重叠部分的图形的面积；
（3）若Rt△AOC沿x轴向右平移t个单位长度（0＜t≤6）得到Rt△A2O2C2 ， Rt△A2O2C2与Rt△OED重叠部分的图形面积记为S，求S与t之间的函数表达式，并写出自变量t的取值范围．

Answer 1

【答案】
（1）

解：∵抛物线y=ax2+bx+c经过点A（﹣3，0），B（9，0）和C（0，4）．

∴设抛物线的解析式为y=a（x+3）（x﹣9），

∵C（0，4）在抛物线上，

∴4=﹣27a，

∴a=﹣ ，

∴设抛物线的解析式为y=﹣ （x+3）（x﹣9）=﹣ x2+ x+4，

∵CD垂直于y轴，C（0，4）

∴﹣ x2+ x+4=4，

∴x=6，

∵D（6，4），

（2）

解：如图1，

∵点F是抛物线y=﹣ x2+ x+4的顶点，

∴F（3， ），

∴FH= ，

∵GH∥A1O1，

∴ ，

∴ ，

∴GH=1，

∵Rt△A1O1F与矩形OCDE重叠部分是梯形A1O1HG，

∴S重叠部分=S△A1O1F﹣S△FGH= A1O1×O1F﹣ GH×FH= ×3×4﹣ ×1× =

（3）

②当3＜t≤6时，如图3，

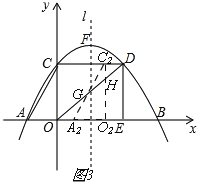
∵C2H∥OC，

∴ ，

∴ ，

∴C2H= （6﹣t），

∴S=S四边形A2O2HG=S△A2O2C2﹣S△C2GH

= OA×OC﹣ C2H×（t﹣3）

= ×3×4﹣ × （6﹣t）（t﹣3）

= t2﹣3t+12

∴当0＜t≤3时，S= t2，当3＜t≤6时，S= t2﹣3t+12

【解析】（1）用待定系数法求抛物线解析式；（2）由GH∥A1O1 ， 求出GH=1，再求出FH，S重叠部分=S△A1O1F﹣S△FGH计算即可；（3）分两种情况①直接用面积公式计算，②用面积差求出即可．此题是二次函数综合题，主要考查了待定系数法求函数解析式，平行线分线段成比例定理，三角形的面积计算，解本题的关键是画出图形．
【考点精析】根据题目的已知条件，利用三角形的面积和平行线分线段成比例的相关知识可以得到问题的答案，需要掌握三角形的面积=1/2×底×高；三条平行线截两条直线，所得的对应线段成比例．