题目内容
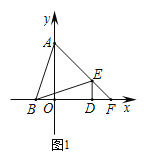
【题目】如图,在矩形ABCD中,点G在AD上,且GD=AB=1,AG=3,点E是线段BC上的一个动点(点E不与点B、C重合),连接GB、GE,△GBE与△GFE关于直线GE对称,当点F落在直线BC和直线DC上时,则所有满足条件的线段BE的长是_____.
【答案】3或![]()
【解析】
△在矩形ABCD中,点E在线段BC上运动时,△GBE关于直线GE对称的△GFE的顶点F在以点G为圆心,以GB为半径的圆上,圆与矩形的边BC、DC所在直线的交点即为点F,连接GF得等腰三角形,作等腰三角形的高,交BC于点E,根据勾股定理、相似三角形的性质,全等即可求BE的长.
解:如图,
△在矩形ABCD中,点E在线段BC上运动时,
△GBE关于直线GE对称的△GFE的顶点F在以点G为圆心,
以GB为半径的圆上,
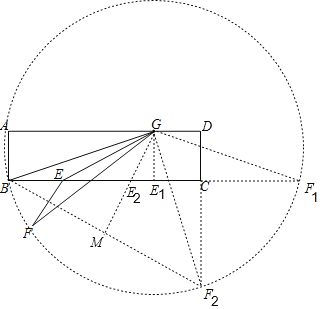
圆与矩形的边BC、DC所在直线的交点分别为点F1、F2,
连接GF1、GF2 得等腰三角形BGF1 和等腰三角形BGF2,
作GE1⊥BF1,GM⊥BF2 交BC于点E2,
①∵四边形ABE1G是矩形,
∴BE1=AG=3;
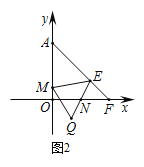
②在矩形ABCD中,GD=AB=1,AG=3,
∴BG=![]() =
=![]() ,
,
∴GF2=![]() ,
,
∵GD=DC=1,
∴DF2=![]() =3,
=3,
∴CF2=DF2﹣DC=2,
∴BF2=![]() =
=![]() =2
=2![]() ,
,
∵GM⊥BF2,
∴BM=![]() BF2=
BF2=![]() ,
,
∵∠BME2=∠BCF2=90°,
∠MBE2=∠CBF2,
∴△BME2∽△BCF2,
∴![]() =
=![]() ,
,
即![]() =
=![]() ,
,
∴BE2=![]() .
.
所以所有满足条件的线段BE的长是3或![]() .
.
故答案为:3或![]() .
.

 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案【题目】我市2013年体育中考考试方案公布后,同学们将根据自己平的运动成绩确定自己的报考项目,下面是小亮同学近期在两个项目中连续五次测试的(得分情况得分统计表得分折线图)
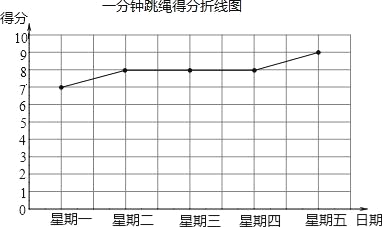
立定跳远测试日期 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
得分 | 7 | 10 | 8 | 9 | 6 |
(1)请根据图表信息,分别计算小亮这两个项目测试成绩的平均数和方差;
(2)根据以上信息,你认为在立定跳远和一分钟跳绳这两个项目中,小亮应选择哪个项目作为体育考试的报考项目?并简述理由.