题目内容
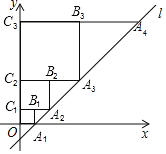
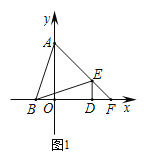
【题目】如图1,在平面直角坐标系中,点A(0,3),点B(-1,0),点D(2,0),DE⊥x轴且∠BED=∠ABD,延长AE交x轴于点F.
(1)求证:∠BAE=∠BEA;
(2)求点F的坐标;
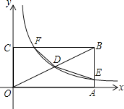
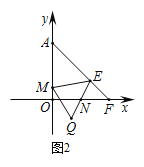
(3)如图2,若点Q(m,-1)在第四象限,点M在y轴的正半轴上,∠MEQ=∠OAF,设AM-MQ=n,求m与n的数量关系,并证明.
【答案】(1)证明见解析;(2)F(3,0);(3)m=n,证明见解析.
【解析】
(1)先证明△ABO≌△BED,从而得出AB=BE,然后根据等边对等角可得出结论;
(2)连接OE,设DF=x,先求出点E的坐标,再根据S△AOE+S△EOF=S△AOF可得出关于x的方程,求出x,从而可得出点F的坐标;
(3)过Q作QP∥x轴交y轴于P,过E作EG⊥OA,EH⊥PQ,垂足分别为G,H,在GA上截取GK=QH,先证明△EQH≌△EKG,再证明△KEM≌△QEM,得出MK=MQ,从而有AM-MQ=AM-MK=AK=n①;连接EP,证明△AEK≌△PEQ,从而有AK=PQ=m②,由①②即可得出结论.
解:(1)∵A(0,3),B(-1,0),D(2,0),
∴OB=1,OD=2,OA=3,
∴AO=BD,
又∠AOB=∠BDE=90°,∠BED=∠ABD,
∴△ABO≌△BED(AAS),
∴BA=BE,
∴∠BAE=∠BEA;
(2)由(1)知,△ABO≌△BED,
∴DE=BO=1,∴E(2,1),
连接OE,设DF=x,
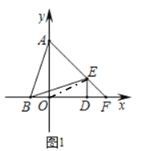
∵S△AOE+S△EOF=S△AOF,
∴3×2×![]() +(2+x)×1×
+(2+x)×1×![]() =3(2+x)×
=3(2+x)×![]() ,
,
∴x=1,
∴点F的坐标为(3,0);
(3)m=n,证明如下:
∵OA=OF=3,∴∠OAF=45°=∠MEQ,
过Q作QP∥x轴交y轴于P,过E作EG⊥OA,EH⊥PQ,垂足分别为G,H,在GA上截取GK=QH,
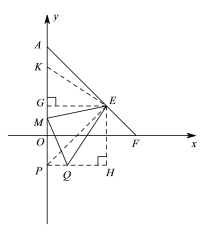
∵Q(m,-1),E(2,1),
∴EG=EH=PH=PG=2,
又GK=QH,∠EGK=∠EQH=90°,
∴△EQH≌△EKG(SAS),
∴EK=EQ,∠GEK=∠HEQ,
∵∠GEH=90°,∠MEQ=45°,∴∠QEH+∠GEM=45°,∴∠GEK+∠GEM=45°,
即∠KEM=45°=∠MEQ,
又EM=EM,
∴△KEM≌△QEM(SAS),∴MK=MQ,
∴AM-MQ=AM-MK=AK=n①,
∴MQ=MG+KG=MG+QH.
连接EP,△EHP为等腰直角三角形,∠EPH=45°,
∴∠EPQ=∠EPA=45°,△EHP为等腰直角三角形,PE=AE,∠PEA=90°,∵∠KEM=∠MEQ=45°,∴∠KEQ=90°,
∴∠AEK=∠PEQ,∠EPQ=∠KAE,
∴△AEK≌△PEQ,
∴AK=PQ=m②,
由①②可得,m=n.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案