题目内容
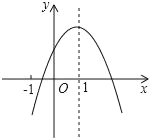
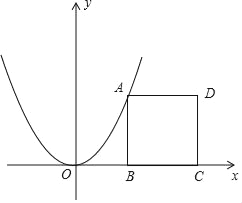
【题目】如图,正方形ABC的顶点A在抛物线y=x2上,顶点B,C在x轴的正半轴上,且点B的坐标为(1,0)
(1)求点D坐标;
(2)将抛物线y=x2适当平移,使得平移后的抛物线同时经过点B与点D,求平移后抛物线解析式,并说明你是如何平移的.
【答案】(1)D(2,1);(2)抛物线向右平移1个单位得到.
【解析】
(1)由点A在抛物线y=x2上,可求出A点坐标,即可求出AB的长度,进而求出AD的长度,即可求得点D的坐标;
(2)设平移后抛物线解析式为:y=(x﹣h)2+k,把B、D两点坐标代入求出h、k的值,即可求得平移后的解析式,即可得新抛物线的顶点坐标根据原抛物线顶点坐标为(0,0)平移即可.
(1)∵B(1,0),点A在抛物线y=x2上,
∴A(1,1),
又∵正方形ABCD中,AD=AB=1,
∴OC=1+1=2,
∴D(2,1);
(2)设平移后抛物线解析式为:y=(x﹣h)2+k,把(1,0),(2,1)代入得:
![]() ,
,
解得:![]() ,
,
∴平移后抛物线解析式为:y=(x﹣1)2,
∴抛物线向右平移1个单位得到.

练习册系列答案
相关题目