题目内容
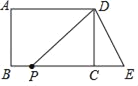
【题目】如图,已知l1∥l2,射线MN分别和直线l1,l2交于A、B,射线ME分别和直线l1,l2交于C、D,点P在A、B间运动(P与A、B两点不重合),设∠PDB=α,∠PCA=β,∠CPD=γ.
(1)试探索α,β,γ之间有何数量关系?说明理由.
(2)如果BD=3,AB=9,AC=6,并且AC垂直于MN,那么点P运动到什么位置时,△ACP≌△BPD说明理由.
(3)在(2)的条件下,当△ACP≌△BPD时,PC与PD之间有何位置关系,说明理由.
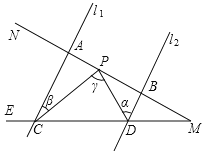
【答案】(1)∠γ=α+∠β;(2)当AP=BD=3,△ACP≌△BPD.(3)CP⊥PD
【解析】
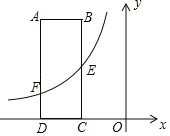
(1)过点P作PF∥l1,根据l1∥l2,可知PF∥l2,故可得出∠α=∠DPF,∠β=∠CPF,由此即可得出结论;
(2)根据平行线的性质得到BD⊥MN,根据全等三角形的性质即可得到结论;
(3)根据全等三角形的性质得到∠ACP=∠DPB,根据垂直的定义即可得到结论.
解:(1)∠γ=α+∠β,
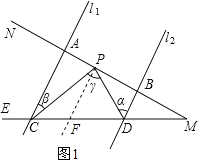
理由:过点P作PF∥l1(如图1),
∵l1∥l2,
∴PF∥l2,
∴∠α=∠DPF,∠β=∠CPF,
∴∠γ=∠DPF+∠CPF=α+∠β;
(2)当AP=BD=3,△ACP≌△BPD,
∵l1∥l2,AC垂直于MN,
∴BD⊥MN,
∴∠CAP=∠PBD=90°,
∵AB=9,
∴PB=6,
∴AC=PB,
在△CAP与△PBD中,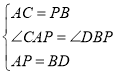 ,
,
∴△ACP≌△BPD,
∴当AP=3时,△ACP≌△BPD;
(3)CP⊥PD,
理由:∵△ACP≌△BPD,
∴∠ACP=∠DPB,
∵∠ACP+∠APC=90°,
∴∠APC+∠DPB=90°,
∴∠CPD=90°,
∴CP⊥PD.

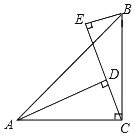
【题目】如图,在平行四边形ABCD中,M、N分别是边AD、BC边上的中点,且△ABM≌△DCM;E、F分别是线段BM、CM的中点.
(1)求证:平行四边形ABCD是矩形.
(2)求证:EF与MN互相垂直.

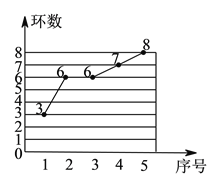
【题目】教练想从甲、乙两名运动员中选拔一人参加射击锦标赛,故先在射击队举行了一场选拔比赛.在相同的条件下各射靶![]() 次,每次射靶的成绩情况如图所示.
次,每次射靶的成绩情况如图所示.
甲射靶成绩的条形统计图
| 乙射靶成绩的折线统计图
|
(![]() )请你根据图中的数据填写下表:
)请你根据图中的数据填写下表:
平均数 | 众数 | 方差 | |
甲 | __________ |
|
|
乙 |
| __________ | __________ |
(![]() )根据选拔赛结果,教练选择了甲运动员参加射击锦标赛,请给出解释.
)根据选拔赛结果,教练选择了甲运动员参加射击锦标赛,请给出解释.