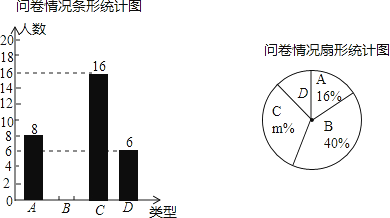
��Ŀ����
����Ŀ����ͼ�٣���ABC�У���ABC=45�㣬AH��BC�ڵ�H����D��AH�ϣ���DH=CH������BD��
��1����֤��BD=AC��
��2������BHD�Ƶ�H��ת���õ���EHF����B��D�ֱ����E��F��Ӧ��������AE��
����ͼ�ڣ�����F����AC��ʱ����F����C�غϣ�����BC=4��tanC=3����AE�ij���
����ͼ�ۣ�����EHF���ɡ�BHD�Ƶ�H��ʱ����ת30��õ�ʱ��������CF��AE�ཻ�ڵ�G������GH����̽���߶�GH��EF֮������ĵ�����ϵ����˵�����ɣ�
���𰸡�
��1��
֤������Rt��AHB�У���ABC=45�㣬
��AH=BH��
�ڡ�BHD�͡�AHC�У�
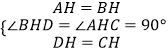 ��
��
���BHD�ա�AHC��
��BD=AC��
��2��
�⣺����ͼ��
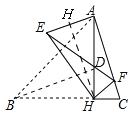
��Rt��AHC��
��tanC=3��
�� ![]() =3��
=3��
��CH=x��
��BH=AH=3x��
��BC=4��
��3x+x=4��
��x=1��
��AH=3��CH=1��
����ת֪����EHF=��BHD=��AHC=90�㣬EH=AH=3��CH=DH=FH��
���EHA=��FHC�� ![]() ��
��
���EHA�ա�FHC��
���EAH=��C��
��tan��EAH=tanC=3��
����H��HP��AE��
��HP=3AP��AE=2AP��
��Rt��AHP��AP2+HP2=AH2��
��AP2+��3AP��2=9��
��AP= ![]() ��
��
��AE= ![]() ��
��
���ɢ��У���AEH�͡�FHC��Ϊ���������Σ�
���GAH=��HCG=90�㣬
���AGQ�ס�CHQ��
�� ![]() ��
��
�� ![]() ��
��
�ߡ�AQC=��GQE��
���AQC�ס�GQH��
�� ![]() =sin30��=
=sin30��= ![]()
����������1�����жϳ�AH=BH�����жϳ���BHD�ա�AHC���ɣ���2�����ȸ���tanC=3�����AH=3��CH=1��Ȼ����ݡ�EHA�ա�FHC���õ���HP=3AP��AE=2AP������ù��ɶ������ɣ������жϳ���AGQ�ס�CHQ���õ� ![]() ��Ȼ���жϳ���AQC�ס�GQH�������Ʊȼ��ɣ������Ǽ��α任�ۺ��⣬��Ҫ��������ת�����ʣ�ȫ�������ε����ʺ��ж������������ε����ʺ��ж������ɶ�����������Ǻ��������壬���������ε��ж������ʣ��Ȿ��Ĺؼ����������������ʺ��ж������ã�
��Ȼ���жϳ���AQC�ס�GQH�������Ʊȼ��ɣ������Ǽ��α任�ۺ��⣬��Ҫ��������ת�����ʣ�ȫ�������ε����ʺ��ж������������ε����ʺ��ж������ɶ�����������Ǻ��������壬���������ε��ж������ʣ��Ȿ��Ĺؼ����������������ʺ��ж������ã�
�����㾫����ͨ��������ù��ɶ����ĸ�������������ε��ж������ʣ�����ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2�����������ε�һ�ж�Ӧ�߶�(��Ӧ�ߡ���Ӧ���ߡ���Ӧ��ƽ���ߡ����Բ�뾶������Բ�뾶�ȣ��ıȵ������Ʊȣ������������ܳ��ıȵ������Ʊȣ���������������ıȵ������Ʊȵ�ƽ�������Խ����⣮