题目内容
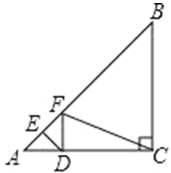
【题目】动手操作:如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=4,点D为边AC上一动点,DE⊥AB交AB于点E,将∠A沿直线DE折叠,点A的对应点为F.当△DFC是直角三角形时,AD的长为_____.
【答案】3
【解析】
由折叠可得∠A=∠AFD,AD=DF,由∠ACB=90°,∠DFC=90°,可证∠BFC=∠B,即CF=BC=4,根据勾股定理可求AD的长.
解:由折叠的性质可得,∠A=∠AFD,AD=DF,
当△DFC是直角三角形时,只有∠DFC=90°这一种情况,
又∵∠ACB=90°,
∴∠A+∠B=90°,∠AFD+∠BFC=90°,
∴∠BFC=∠B,
∴FC=BC=4,
在Rt△DFC中,CD2=DF2+FC2,
∴(8AD)2=AD2+42,
∴AD=3,
故答案为3.

练习册系列答案
相关题目