题目内容
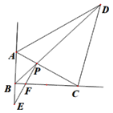
【题目】(1)如图1,已知△ABC为等边三角形,动点D在边AC上,动点P在边BC上,若这两点分别从C、B点同时出发,以相同的速度由C向A和由B向C运动,连结AP、BD交于Q,两点运动的过程中,AP=BD成立吗?请证明你的结论.
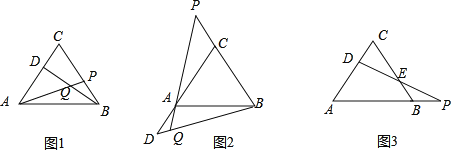
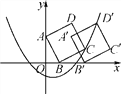
(2)如果把原题中的“动点D在边AC上,动点P在边BC上,”改为:“动点D在射线CA上、动点P在射线BC上运动,”其他条件不变,如图2所示,AP=BD还成立吗?说明理由,并求出∠BQP的大小.
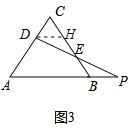
(3)如果把原题中的“动点P在边BC上”,改为“动点P在射线AB上运动”,连结DP交BC于E,其他条件不变,如图3,则动点D、P在运动过程中,请你写出DE与PE的数量关系.
【答案】(1)成立,理由见解析;(2)AP=BD成立,理由见解析, 60°;(3)DE=PE,理由见解析.
【解析】
(1)根据等边三角形的性质得到∠C=∠ABP=60°,AB=BC,证明△ABP≌△BCD,根据全等三角形的性质解答;
(2)证明△ABP≌△BCD,根据全等三角形的性质得到AP=BD,根据三角形的外角的性质求出∠BQP;
(3)作DH∥AB交BC于H,得到△CDH为等边三角形,得到DH=CD,证明△HDE≌△BPE,根据全等三角形的性质证明.
解:(1)成立,
证明:∵△ABC是等边三角形,
∴∠C=∠ABP=60°,AB=BC,
由题意得,CD=BP,
在△ABP和△BCD中,
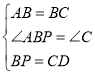 ,
,
∴△ABP≌△BCD,
∴AP=BD;
(2)AP=BD成立,
理由如下:由题意得,CP=AD,
∴CP+BC=AD+AC,即BP=CD,
在△ABP和△BCD中,
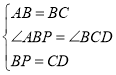 ,
,
∴△ABP≌△BCD,
∴AP=BD,∠APB=∠BDC,
∵∠APC+∠PAC=∠ACB=60°,∠DAQ=∠PAC,
∴∠BQP=∠DAQ+∠BDC=60°;
(3)DE=PE,
理由如下:作DH∥AB交BC于H,
∵△ABC为等边三角形,DH∥AB
∴∠CDH=∠A=60°,∠CHD=∠CBA=60°,∠HDE=∠P,
∴△CDH为等边三角形,
∴DH=CD,
∵CD=BP,
∴DH=BP,
在△HDE和△BPE中,
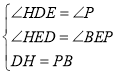 ,
,
∴△HDE≌△BPE,
∴DE=PE.