题目内容
【题目】阅读下面材料:
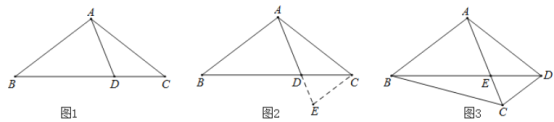
小腾遇到这样一个问题:如图1,在![]() 中,点
中,点![]() 在线段
在线段![]() 上.
上.![]() ,
,![]() ,
,![]() ,
,![]() .求
.求![]() 的长.
的长.
小腾发现,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,通过构造
,通过构造![]() ,经过推理和计算能够使问题得到解决(如图2).
,经过推理和计算能够使问题得到解决(如图2).
发现:![]() 的度数为 ,
的度数为 ,![]() 的长为
的长为
探究:参考小腾思考问题的方法,解决问题:
如图3,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,求
,求![]() ,
,![]() 的长.
的长.
【答案】发现:∠ACE的度数为75°,AC的长为3;探究:![]() ,
,![]()
【解析】
发现:根据平行线的性质得到∠E=∠BAD=75°,根据三角形内角和定理即可得出![]() ,证明△ABD∽△DCE,根据相似三角形的性质得出AC的长;
,证明△ABD∽△DCE,根据相似三角形的性质得出AC的长;
探究:过点D作DF⊥AC于点F,证明△ABE∽△FDE,根据相似三角形的性质求出EF、AF,根据正切的概念求出DF,根据勾股定理计算即可.
发现:∵CE∥AB,
∴∠E=∠BAD=75°,
∴∠ACE=180°-∠CAD-∠E=180°-75°-30°=75°,
∵∠E=75°,∴∠ACE=∠E,
∴AC=AE,
∵CE∥AB,BD=2DC,
∴△ABD∽△DCE,
∴![]()
∴AD=2DE,
∴DE=1,∴AE=3,
∴AC=3;∴AD=2DE,
∵AE=AD+DE=3,
∴AC=AE=3;
故答案为:75,3
探究:过点D作DF⊥AC于F,如图

∵ ∠BAC=90°,
∴ AB∥DF,∴ △ABE∽△FDE.
∴ ![]()
∴EF=1 , AB=2DF.
∴AF=3
在Rt△ACD中,∠CAD=30°
设DF=x,则AD=2x,
由勾股定理得![]() ,解得
,解得![]() ,∴
,∴![]()
∵ 在△ACD中,∠CAD=30°,∠ADC=75°,
∴ ∠ACD=75°,∴ AC=AD
∵AD=2DF ,AB=2DF
∴AD=AB
∴AB=AC
![]()

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案
相关题目