题目内容
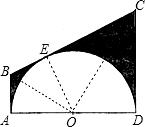
如图,半圆O的直径AD=12cm,AB,BC,CD分别与半圆O切于点A,E,D.
(1)设AB=x,CD=y,求y与x之间的函数关系式;
(2)如果CD=6,判断四边形ABCD的形状;
(3)如果AB=4,求图中阴影部分的面积.
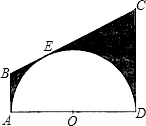
(1)设AB=x,CD=y,求y与x之间的函数关系式;
(2)如果CD=6,判断四边形ABCD的形状;
(3)如果AB=4,求图中阴影部分的面积.

(1)连接OB、OE、OC
∵AB,BC分别与半圆O切于点A,E,∴BE=BA,∠OEB=∠OAB=90°
∴△OAB≌△OEB
∴∠EOB=∠AOB
同理,∵BC,CD分别与半圆O切于点E,D
∴△COE≌△COD
∴∠COD=∠COE
∵∠AOB+∠EOB+∠COE+∠COD=180°
∴∠BOE+∠COE=90°
∴OB⊥OC
∵OB2=OA2+AB2=36+x2;OC2=OD2+CD2=36+y2;
∵BE=AB=x,CE=CD=y;BC=x+y.
∴(x+y)2=36+x2+36+y2;
∴xy=36;
化简可得:y=
;
(2)若CD=6,又有半圆O的直径AD=12cm;即OE=6;故OE∥DC∥AB.
则四边形ABCD的形状是矩形;
(3)过点B作BF⊥CD于F,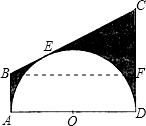
∵BA是半圆O的切线,AD是半圆O的直径,
∴BA⊥AD.
又∵CD⊥AD,
∴四边形ABFD是矩形,
∴BF=AD=12,FD=BA=4.
∴CF=5,
∵CB、BA和CD都是半圆O的切线,
∴CE=CD=9,BE=BA=4.
∴CB=CE+EB=13,
∵S半圆=
π×62=18π,S梯形ABCD=
(4+9)•12=78,
∴S阴=S梯-S半圆=78-18π
说明:(1)(4分);(2)(3分);(3)(5分).
∵AB,BC分别与半圆O切于点A,E,∴BE=BA,∠OEB=∠OAB=90°
∴△OAB≌△OEB
∴∠EOB=∠AOB
同理,∵BC,CD分别与半圆O切于点E,D
∴△COE≌△COD
∴∠COD=∠COE
∵∠AOB+∠EOB+∠COE+∠COD=180°
∴∠BOE+∠COE=90°
∴OB⊥OC
∵OB2=OA2+AB2=36+x2;OC2=OD2+CD2=36+y2;
∵BE=AB=x,CE=CD=y;BC=x+y.
∴(x+y)2=36+x2+36+y2;
∴xy=36;
化简可得:y=
| 36 |
| x |
(2)若CD=6,又有半圆O的直径AD=12cm;即OE=6;故OE∥DC∥AB.
则四边形ABCD的形状是矩形;
(3)过点B作BF⊥CD于F,

∵BA是半圆O的切线,AD是半圆O的直径,
∴BA⊥AD.
又∵CD⊥AD,
∴四边形ABFD是矩形,
∴BF=AD=12,FD=BA=4.
∴CF=5,
∵CB、BA和CD都是半圆O的切线,
∴CE=CD=9,BE=BA=4.
∴CB=CE+EB=13,
∵S半圆=
| 1 |
| 2 |
| 1 |
| 2 |
∴S阴=S梯-S半圆=78-18π
说明:(1)(4分);(2)(3分);(3)(5分).


练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
 A点左侧)是双曲线y=
A点左侧)是双曲线y=