题目内容
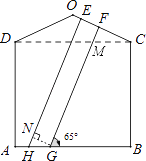
【题目】（本题满分10分）一幢房屋的侧面外墙壁的形状如图所示，它由等腰三角形OCD和矩形ABCD组成，∠OCD=25°，外墙壁上用涂料涂成颜色相同的条纹，其中一块的形状是四边形EFGH，测得FG∥EH，GH=2.6m，∠FGB=65°。
（1）求证：GF⊥OC；
（2）求EF的长（结果精确到0.1m）。
（参考数据：sin25°=cos65°≈0.42，cos25°=sin65°≈0.91）
【答案】（1）在四边形BCFG中，∠GFC=360°-90°-65°-（90°+25°）=90°
则GF⊥OC
（2）如图，作FM∥GH交EH与M，则有平行四边形FGHM,
∴FM=GH=2.6m，∠EFM=25°
∵FG∥EH，GF⊥OC
∴EH⊥OC
在Rt△EFM中：
EF=FM·cos25°≈2.6×0.91=2.4m
【解析】
试题（1）根据
四边形
是矩形，
得出
，即可得出答案．
（2）根据矩形的判定得出
，再利用解直角三角形的知识得出
的长．
试题解析：(1)证明：CD与FG交于点M，
∵,四边形ABCD是矩形,
∴
∴GF⊥CO；
(2)作GN⊥EH于点N，
∴四边形ENGF是矩形；
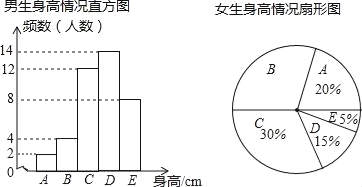
发散思维新课堂系列答案【题目】为了了解某校学生的身高状况，随机对该校男生、女生的身高进行抽样调查．已知抽取的样本中，男生、女生的人数相同，根据所得数据绘制如图所示的统计图表：
组别 | 身高（cm） |
A | x＜150 |
B | 150≤x＜155 |
C | 155≤x＜160 |
D | 160≤x＜165 |
E | x≥165 |
已知女生身高在A组的有8人，根据图表中提供的信息，回答下列问题：
（1）男生身高的中位数落在 组（填组别字母序号）；
（2）在样本中，身高在150≤x＜155之间的人数共有 人，身高人数最多的在 组（填组别序号）；
（3）已知该校共有男生400人、女生420人，请估计身高不足160cm的学生约有多少人？
