Question

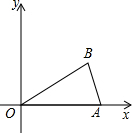如图，已知O为坐标原点，∠AOB=30°，∠ABO=90°，且点A的坐标为（2，0）．
（1）求直线AB的解析式；
（2）若二次函数y=ax²+bx+c的图象经过A、B、O三点，求此二次函数的解析式；
（3）结合（1）（2）及图象，直接写出使一次函数的值大于二次函数的值的x的取值范围．

Answer 1

分析：（1）先过B作BD⊥x轴于D，在Rt△AOB中利用含有30°角的直角三角形的性质，易求AB，同理可求AD，结合勾股定理可求BD，从而易求点B的坐标，然后把B、A两点坐标代入一次函数解析式，易得关于ab的二元一次方程组，解可求ab，从而可得一次函数解析式；
（2）把A、B、O三点坐标代入二次函数解析式，可得关于a、b、c的三元一次方程组，解即可求a、b、c，从而可得二次函数解析式；
（3）根据图可知x的取值范围．

解答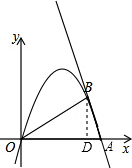：解：（1）∵A的坐标为（2，0），
∴OA=2，
∵∠AOB=30°，∠ABO=90°，
∴AB=1，∠BAD=60°，
过B作BD⊥x轴于D，
在Rt△ABD中，AB=1，∠BAD=60°，
∴∠ABD=30°，
∴AD=

1

2

，
∴BD=

12-( 1 2 )2

=

3

2

，
∴OD=2-

1

2

=

3

2

，
∴B点的坐标是（

3

2

，

3

2

），
设直线AB的解析式是y=ax+b，
把（2，0）（

3

2

，

3

2

）代入y=ax+b中，得

2a+b=0 3 2 a+b= 3 2

，
解得

a=- 3 b=2 3

，
∴一次函数的解析式是y=-

3

x+2

3

；
（2）把（2，0）、（

3

2

，

3

2

）、（0，0）代入二次函数y=ax²+bx+c中，得

4a+2b+c=0 9 4 a+ 3 2 b+c= 3 2 c=0

，
解得

a=- 2 3 3 b= 4 3 3 c=0

，
∴二次函数解析式是y=-

2 3

3

x2+

4 3

3

x；
（3）据图观察可知当x＜

3

2

或x＞2时，一次函数的值大于二次函数的值．

点评：本题考查了待定系数法求函数解析式、二次函数与不等式组，解题的关键是掌握含有30°角的直角三角形的性质、勾股定理、解方程组，并会观察函数图象，比较大小．