题目内容
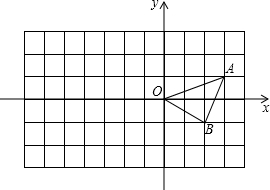
如图,已知O是坐标原点,A、B的坐标分别为(3,1)、(2,-1).(1)在y轴的左侧以O为位似中心作△OAB的位似三角形OCD.(要求:新图与原图的相似比为2);
(2)分别写出A、B的对应点C、D的坐标;
(3)求△OCD的面积;
(4)如果△OAB内部一点M的坐标为(m,n),写出点M在△OCD内的对应点N的坐标.
分析:(1)根据位似变换的性质,即可画出位似三角形OCD;
(2)根据位似变换的性质,即可求得:A、B的对应点C、D的坐标;
(3)首先构造直角梯形CDEF,由S△OCD=S梯形CDEF-S△ODE-S△OCF,即可求得△OCD的面积;
(4)结合图形,由位似变化的性质,即可求得:点M在△OCD内的对应点N的坐标.
(2)根据位似变换的性质,即可求得:A、B的对应点C、D的坐标;
(3)首先构造直角梯形CDEF,由S△OCD=S梯形CDEF-S△ODE-S△OCF,即可求得△OCD的面积;
(4)结合图形,由位似变化的性质,即可求得:点M在△OCD内的对应点N的坐标.
解答:解:(1)如图:
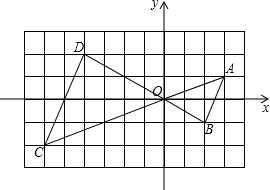
(2)C(-6,-2),D(-4,2);
(3)
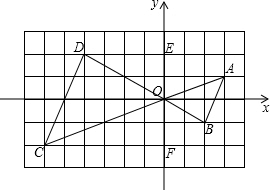
∵DE=4,OE=2,OF=2,EF=4,CF=6,
∴S△OCD=S梯形CDEF-S△ODE-S△OCF=
(DE+CF)•EF-
DE•OE-
CF•OF,
=
×(4+6)×4-
×4×2-
×6×2,
=10;
(4)∵△OAB内部一点M的坐标为(m,n),
∴点M在△OCD内的对应点N的坐标为(-2m,-2n).

(2)C(-6,-2),D(-4,2);
(3)

∵DE=4,OE=2,OF=2,EF=4,CF=6,
∴S△OCD=S梯形CDEF-S△ODE-S△OCF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=10;
(4)∵△OAB内部一点M的坐标为(m,n),
∴点M在△OCD内的对应点N的坐标为(-2m,-2n).
点评:此题考查了位似变换的性质,还考查了学生的动手能力.题目比较简单,注意数形结合思想的应用.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
 24、如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1).
24、如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1).

 作图题:如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1).
作图题:如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1).