题目内容

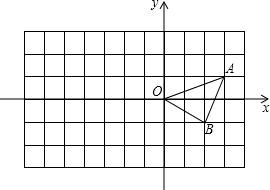
如图，已知O是坐标原点，A、B、C的坐标分别为（0，-3）、（4，-2）、（3，1），以O为位似中心作△ABC的位似三角形（只作一个图形即可），要求：新图与原图的相似比为2，并写出点B和点C的对应点的坐标．
分析：延长AO到A′，使OA′=2AO，延长BO到B′，使OB′=2BO，延长CO到C′，使OC′=2CO，然后顺次连接A′、B′、C′即可得解；
或：延长OA到A′，使OA′=2AO，延长OB到B′，使OB′=2BO，延长OC到C′，使OC′=2CO，然后顺次连接A′、B′、C′即可得解．
解答：解：如图所示，△A′B′C′即为所求作的三角形，
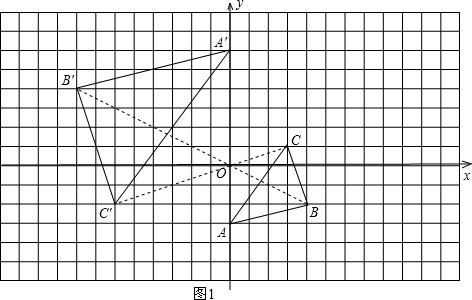
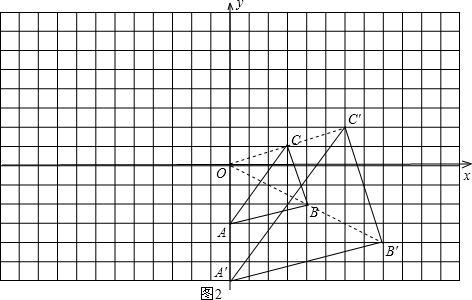
图1中，点B和点C的对应点B′、C′的坐标分别为（-8，4）、（-6，-2），
图2中，点B和点C的对应点B′、C′的坐标分别为（8，-4）、（6，2）．
点评：本题考查了利用位似变换作图，根据网格结构找出对应点的位置是解题的关键，需要注意，本题可以作出两个相似三角形，作出其中的任何一个都算正确．
练习册系列答案
相关题目
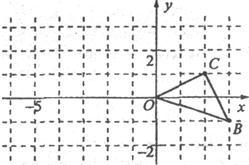24、如图，已知O是坐标原点，B、C两点的坐标分别为（3，-1）、（2，1）．
（1）以0点为位似中心在y轴的左侧将△OBC放大到两倍（即新图与原图的相似比为2），画出图形；
（2）分别写出B、C两点的对应点B′、C′的坐标；
（3）如果△OBC内部一点M的坐标为（x，y），写出M的对应点M′的坐标．
20、（1）以下列正方形网络的交点为顶点，分别画出两个相似比不为1的相似三角形，使它们：
（1）都是直角三角形；（2）都是锐角三角形；（3）都是钝角三角形．

（2）如图，已知O是坐标原点，B、C两点的坐标分别为（3，-1）、（2，1）．
①以0点为位似中心在y轴的左侧将△OBC放大到两倍（即新图与原图的相似比为2），画出图形；
②分别写出B、C两点的对应点B′、C′的坐标；
③如果△OBC内部一点M的坐标为（x，y），写出M的对应点M′的坐标．
如图，已知O是坐标原点，A、B的坐标分别为（3，1）、（2，-1）．
（1）在y轴的左侧以O为位似中心作△OAB的位似三角形OCD．（要求：新图与原图的相似比为2）；
（2）分别写出A、B的对应点C、D的坐标；
（3）求△OCD的面积；
（4）如果△OAB内部一点M的坐标为（m，n），写出点M在△OCD内的对应点N的坐标．
精英家教网
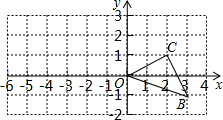作图题：如图，已知O是坐标原点，B、C两点的坐标分别为（3，-1）、（2，1）．
（1）以0点为位似中心在y轴的左侧将△OBC放大到两倍（即新图与原图的相似比为2，画出图形；
（2）分别写出B、C两点的对应点B′、C′的坐标．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网