题目内容
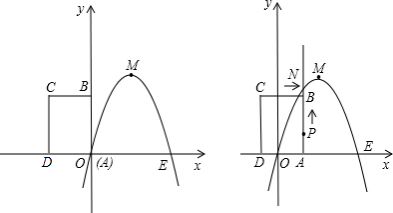
 如图,已知抛物线经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2),
如图,已知抛物线经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2),(1)求该抛物线的解析式;
(2)现将它向右平移m(m>0)个单位,所得抛物线与x轴交于C、D两点,与原抛物线交于点P,△CDP的面积为S,求S关于m的关系式;
(3)当m=2时,点Q为平移后的抛物线的一动点,是否存在这样的⊙Q,使得⊙Q与两坐标轴都相切?若存在,求出点Q的坐标;若不存在,请说明理由.
分析:(1)利用顶点式解析式设出抛物线解析式,然后把原点坐标代入进行计算即可得解;
(2)根据平移规律,先写出平移后的解析式的顶点坐标,然后写出平移后的抛物线解析式,与原抛物线解析式联立求解即可得到点P的坐标,根据抛物线的对称性求出OA的长度,然后根据平移的性质得到CD的长度,最后分①0<m<2时,点P在第一象限,②m>2时,点P在第四象限,分别利用三角形的面积公式列式整理即可得解;
(3)假设存在点Q,根据抛物线的解析式设出点Q的坐标,然后根据点Q到x轴与y轴的距离相等解方程即可.
(2)根据平移规律,先写出平移后的解析式的顶点坐标,然后写出平移后的抛物线解析式,与原抛物线解析式联立求解即可得到点P的坐标,根据抛物线的对称性求出OA的长度,然后根据平移的性质得到CD的长度,最后分①0<m<2时,点P在第一象限,②m>2时,点P在第四象限,分别利用三角形的面积公式列式整理即可得解;
(3)假设存在点Q,根据抛物线的解析式设出点Q的坐标,然后根据点Q到x轴与y轴的距离相等解方程即可.
解答:解:(1)∵抛物线顶点坐标为(1,2),
∴设抛物线解析式为y=a(x-1)2+2,
又∵抛物线经过原点,
∴a(0-1)2+2=0,
解得a=-2,
∴抛物线的解析式为y=-2(x-1)2+2;
(2)抛物线向右平移m个单位,则顶点坐标为(1+m,2),
∴平移后的抛物线解析式为y=-2(x-1-m)2+2,
与原抛物线解析式联立得,
,
解得
,
又∵原抛物线的顶点坐标为(1,2),
∴点A、O关于直线x=1对称,
∴点A的坐标为(2,0),
∴AO=2,
∴CD=AO=2,
①0<m<2时,点P在第一象限,
S=
×2×(-
m2+2)=-
m2+2,
②m>2时,点P在第四象限,
S=
×2×[-(-
m2+2)]=
m2-2;
综上所述,S关于m的关系式为S=
;
(3)根据(2),当m=2时,平移后的抛物线解析式为y=-2(x-1-2)2+2=-2(x-3)2+2=-2x2+12x-16,
假设存在⊙Q,使得⊙Q与两坐标轴都相切,设点Q的坐标为(x,-2x2+12x-16),
则x=|-2x2+12x-16|,
∴x=-2x2+12x-16①或x=-(-2x2+12x-16)②,
整理①得,2x2-11x+16=0,
△=112-4×2×16=121-128=-7<0,
方程无解,
整理②得,2x2-13x+16=0,
解得x=
=
=
,
∴当x=
时,y=
,
当x=
时,y=
,
∴点Q的坐标为(
,
)或(
,
).
∴设抛物线解析式为y=a(x-1)2+2,
又∵抛物线经过原点,
∴a(0-1)2+2=0,
解得a=-2,
∴抛物线的解析式为y=-2(x-1)2+2;
(2)抛物线向右平移m个单位,则顶点坐标为(1+m,2),

∴平移后的抛物线解析式为y=-2(x-1-m)2+2,
与原抛物线解析式联立得,
|
解得
|
又∵原抛物线的顶点坐标为(1,2),
∴点A、O关于直线x=1对称,
∴点A的坐标为(2,0),
∴AO=2,
∴CD=AO=2,

①0<m<2时,点P在第一象限,
S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
②m>2时,点P在第四象限,
S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
综上所述,S关于m的关系式为S=
|
(3)根据(2),当m=2时,平移后的抛物线解析式为y=-2(x-1-2)2+2=-2(x-3)2+2=-2x2+12x-16,
假设存在⊙Q,使得⊙Q与两坐标轴都相切,设点Q的坐标为(x,-2x2+12x-16),
则x=|-2x2+12x-16|,
∴x=-2x2+12x-16①或x=-(-2x2+12x-16)②,
整理①得,2x2-11x+16=0,
△=112-4×2×16=121-128=-7<0,
方程无解,
整理②得,2x2-13x+16=0,
解得x=
-b±
| ||
| 2a |
13±
| ||
| 2×2 |
13±
| ||
| 4 |
∴当x=
13-
| ||
| 4 |
-13+
| ||
| 4 |
当x=
13+
| ||
| 4 |
-13-
| ||
| 4 |
∴点Q的坐标为(
13-
| ||
| 4 |
-13+
| ||
| 4 |
13+
| ||
| 4 |
-13-
| ||
| 4 |
点评:本题是对二次函数的综合考查,待定系数法求函数解析式,两函数图象交点的求解方法,三角形的面积,以及直线与圆相切,则圆心到直线的距离等于半径的利用,综合性较强,难度较大,注意求解时需要分情况讨论.

练习册系列答案
相关题目
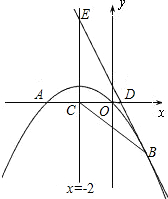 2x+1经过抛物线上一点B(2,m),且与y轴.直线x=-2分别交于点D、E.
2x+1经过抛物线上一点B(2,m),且与y轴.直线x=-2分别交于点D、E. (2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.
(2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1. 如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E,
如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E,