Question

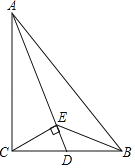
【题目】如图，在Rt△ABC中，∠ACB＝90°，点D是边BC的中点，联结AD．过点C作CE⊥AD于点E，联结BE．

（1）求证：BD2＝DEAD；

（2）如果∠ABC＝∠DCE，求证：BDCE＝BEDE．

Answer 1

【答案】（1）证明见解析；（2）证明见解析．

【解析】

（1）证明△CDE∽△ADC推出，可得CD2＝DEDA即可解决问题．

（2）利用相似三角形的性质首先证明AC＝BE，再证明△ACE∽△CDE，可得，可得即可解决问题．

解：

（1）证明：如图1中，

∵CE⊥AD，

∴∠CED＝∠ACD＝90，

∵∠CDE＝∠ADC，

∴△CDE∽△ADC

∴，

∴CD2＝DEDA，

∵DB＝CD，

∴∴BD2＝DEDA．

（2）解：如图2中，

∵BD2＝DEDA，

∴，

∵∠CDE＝∠ADB，

∴△BDE∽△ADB，

∴∠DEB＝∠ABC，

∵∠ABD＝∠ECD，

∴∠BED＝∠BCE，

∵∠EBD＝∠CBE，

∴△EBD∽△CBE，

∴，

∴BE2＝BDBC，

∵CD＝BD，

∴BE2＝2CD2，

∵∠DCE+∠ACE＝90，∠CAD+∠ACE＝90，

∴∠CAD＝∠ECD＝∠ABC，

∵∠ACD＝∠BCA，

∴△ACD∽△BCA，

∴，

∴AC2＝CDCB＝2CD2，

∴AC＝BE，

∵△ACE∽△CDE，

∴，

∴，

∴BDCE＝BEDE．