题目内容
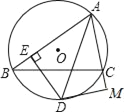
【题目】如图,在圆O中,弦AC,BD相交于点M,且∠A=∠B
(1)求证:AC=BD;
(2)若OA=4,∠A=30°,当AC⊥BD时,求弧CD的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)(1)延长AO交⊙O于点F,连接CF,延长BO交⊙O于点E,连接DE,证明△DEB≌△CFA即可得到结论;
(2)延长AO交⊙O于点F,连接CF,延长BO交⊙O于点E,连接DE,CD,OD,OC,先求得∠COA=120°,再求出∠EOA=30°,即可得到∠COD=30°,再根据弧长公式计算.
证明:(1)延长AO交⊙O于点F,连接CF,延长BO交⊙O于点E,连接DE,
∵BE,AF是⊙O的直径,
∴∠EDB=∠FCA=90°.
在△DEB与△CFA中,
∵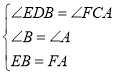 ,
,
∴△DEB≌△CFA(AAS),
∴AC=BD;
(2)延长AO交⊙O于点F,连接CF,延长BO交⊙O于点E,连接DE,CD,OD,OC,
∵∠A=30°,OA=OC,
∴∠COA=180°﹣30°﹣30°=120°.
∵∠A=∠B=30°,AC⊥BD,
∴∠EOA+∠A=60°,
∴∠EOA=30°,
∴∠DOE=60°,
∴∠COD=30°,
∴![]() .
.


练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
【题目】二次函数y=ax![]() +bx+c的x,y的对应值如下表:
+bx+c的x,y的对应值如下表:
x | … | -1 |
| 0 |
| 1 |
| 2 | … |
y | … | -1 |
| m |
| 1 |
| n | … |
下列关于该函数性质的判断:①该二次函数有最大值;②当x>0时,函数y随x的增大而减小;③不等式y<﹣1的解集是﹣1<x<2;④关于x的一元二次方程ax2+bx+c=0的两个实数根分别位于﹣1<x<![]() 和
和![]() <x<2之间.其中正确结论的个数有( )
<x<2之间.其中正确结论的个数有( )
A.1个B.2个C.3个D.4个