题目内容
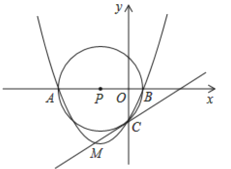
【题目】如图,在平面直角坐标系中,坐标原点为O,A点坐标为(-4,0),B点坐标为(1,0),以AB的中点P为圆心,AB为直径作⊙P与y轴的负半轴交于点C.
(1)求经过A、B、C三点的抛物线对应的函数表达式;
(2)设M为(1)中抛物线的顶点,试说明直线MC与⊙P的位置关系,并证明你的结论;
(3)在第二象限中是否存在的一点Q,使得以A,O,Q为顶点的三角形与△OBC相似.若存在,请求出所有满足的Q点坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)相切,见解析;(3)存在,(-4,8)、(-4,2)、
;(2)相切,见解析;(3)存在,(-4,8)、(-4,2)、![]() 、
、![]()
【解析】
(1)由A点坐标和B点坐标,可以求出AB的长度,即圆的直径可以求出,进而得出圆的半径长度,根据B点坐标,求出OP的长,再根据勾股定理求出C点坐标,设出二次函数交点式,将C点坐标代入求解即可.
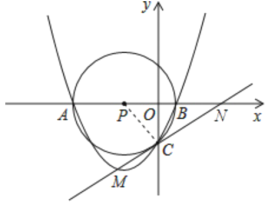
(2)直线与圆的位置关系无非是相切或不相切,可连接PC,证PC是否与MC垂直即可.本题可先求出直线MC与x轴的交点N的坐标,然后分别求出PN,PC,CN的长,用勾股定理逆定理进行判断.
(3)△OBC与△AOQ相似,△OBC与△AQO相似,△OBC与△QAO相似,△OBC与△QOA相似,四种情况讨论根据三角形相似的性质列出关系式求解即可.
 y个
y个
(1)连接PC,.
∵A(-4,0),B(1,0)
∴AB=5,
∵P是AB的中点,且是![]() 的圆心
的圆心
∴PC=PA=2.5,OP=4-2.5=1.5.
∴![]()
∴C(0,-2).
设经过A.B.C三点的抛物线为
![]()
![]()
![]() .
.
抛物线为![]()
(2)直线MC与![]() 相切.
相切.
将![]() 配方,得
配方,得
![]()
∴顶点M为![]()
设直线MC为y=kx+b,则有
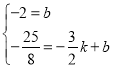
解得
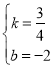
∴直线MC为![]()
设MC与x轴交于点N,
在![]() 中,令y=0,得
中,令y=0,得![]()
![]()
![]()
![]()
∴MC与OP相切.
(3)当△OBC与△AOQ相似,
OB:OC=AO:AQ,
即1:2=4:AQ,
解得AQ=8,
则Q点坐标为(-4,8);
当△OBC与△AQO相似,
OB:OC=AQ:AO,
即1:2=AQ:4,
解得AQ=2,
则Q点坐标为(-4,2);
当△OBC与△QAO相似,
OC:BC=QO:AO,
即![]() ,
,
解得![]() ,
,
则Q点横坐标为![]()
纵坐标为![]() .
.
则Q点坐标为![]()
当△OBC与△QO4相似,
OB:BC=QO:AO,
即![]() ,
,
解得![]() ,
,
则Q点横坐标为![]()
纵坐标为![]()
则Q点坐标为![]()
综上所述,使得以A,O,Q为顶点的三角形与△OBC相似,
所有满足的Q点坐标为:
(-4,8)、(-4,2)、![]() 、
、![]()

 阅读快车系列答案
阅读快车系列答案【题目】二次函数y=ax![]() +bx+c的x,y的对应值如下表:
+bx+c的x,y的对应值如下表:
x | … | -1 |
| 0 |
| 1 |
| 2 | … |
y | … | -1 |
| m |
| 1 |
| n | … |
下列关于该函数性质的判断:①该二次函数有最大值;②当x>0时,函数y随x的增大而减小;③不等式y<﹣1的解集是﹣1<x<2;④关于x的一元二次方程ax2+bx+c=0的两个实数根分别位于﹣1<x<![]() 和
和![]() <x<2之间.其中正确结论的个数有( )
<x<2之间.其中正确结论的个数有( )
A.1个B.2个C.3个D.4个