��Ŀ����
��Щ����ֵ�������ͨ������ĸ��������ת������ʽ����������������Ķ�����Ľ�����̣��ٽ���������⣮
������x=123456789��123456786��y=123456788��123456787���ԱȽ�x��y�Ĵ�С��
�⣺��123456788=a����ôx=(a��1)(a-2)=a2-a-2��y=a(a-1)=a2-a��
��x-y=(a2-a-2)-(a2-a)=-2��0����x��y��
�������ѧ�����ַ���������������һ�ɣ����У�
���⣺����1��35��0��35��2��7-1��353-1��35��0��352��
������x=123456789��123456786��y=123456788��123456787���ԱȽ�x��y�Ĵ�С��
�⣺��123456788=a����ôx=(a��1)(a-2)=a2-a-2��y=a(a-1)=a2-a��
��x-y=(a2-a-2)-(a2-a)=-2��0����x��y��
�������ѧ�����ַ���������������һ�ɣ����У�
���⣺����1��35��0��35��2��7-1��353-1��35��0��352��
-1��35��
���������������0��35��2��7����1��35�й�ϵ������1��35=x����ô0��35=x-1��2��7=2x��Ȼ����м��㣮
��1��35=x����ô0��35=x-1��2��7=2x��
ԭʽ=x��x-1��•2x-x3-x��x-1��2��
=��2x3-2x2��-x3-x��x2-2x+1����
=2x3-2x2-x3-x3+2x2-x��
=-x
=-1��35��

��ϰ��ϵ�д�
 �����ߴ���ϵ�д�
�����ߴ���ϵ�д�
�����Ŀ

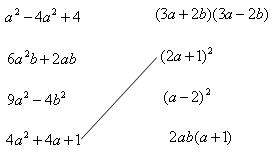
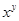 = ��
= ��



 ��n=1��2��3��������b1=2(1-a1)��b2=2(1-a1)(1-a2)����bn=2(1-a1)(1-a2)(1-an)����ͨ�������Ʋ��bn�ı���ʽbn= �����ú�n�Ĵ���ʽ��ʾ����
��n=1��2��3��������b1=2(1-a1)��b2=2(1-a1)(1-a2)����bn=2(1-a1)(1-a2)(1-an)����ͨ�������Ʋ��bn�ı���ʽbn= �����ú�n�Ĵ���ʽ��ʾ����
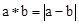 ������
������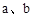 Ϊʵ������
Ϊʵ������ ��
��