题目内容
若x2+y2+2x-4y+5=0,则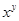 = .
= .
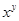 = .
= .1
试题分析:将已知等式左边的5变形为4+1,结合后利用完全平方公式变形,利用两个非负数之和为0,两非负数分别为0得到关于x与y的一元一次方程,分别求出一次方程的解得到x与y的值,代入所求式子中计算,即可得到结果.
试题解析:将x2+y2-4y+2x+5=0变形得:x2+2x+1+y2-4y+1=0,即(x+1)2+(y-2)2=0,
∴y-2=0且x+1=0,
解得:y=2,x=-1,
则xy=(-1)2=1.

练习册系列答案
相关题目
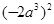
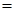 。
。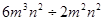 = 。
= 。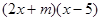 的展开式中不含x的一次项,则m=____________
的展开式中不含x的一次项,则m=____________ ,a-b=
,a-b= ,则a+b的值为( )
,则a+b的值为( )