题目内容
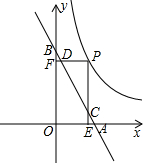 (2013•永春县质检)如图所示,直线AB与x轴交于点A(3,0),与y轴交于点B(0,4),点P为双曲线y=
(2013•永春县质检)如图所示,直线AB与x轴交于点A(3,0),与y轴交于点B(0,4),点P为双曲线y=| 6 |
| x |
(1)AB=
5
5
;(2)AD•BC=
| 25 |
| 2 |
| 25 |
| 2 |
分析:(1)直接利用勾股定理求得AB的长即可;
(2)首先求得直线AB的解析式,然后设P的坐标是(m,
),据此即可求得线段AD、BC的长,从而求解.
(2)首先求得直线AB的解析式,然后设P的坐标是(m,
| 6 |
| m |
解答:解:(1)∵直线AB与x轴交于点A(3,0),与y轴交于点B(0,4),
∴OA=3,OB=4,
∴由勾股定理得AB=
=5,;
(2):设直线AB的解析式是y=kx+b,
则:
解得:
则直线的解析式是:y=-
x+4.
设P的坐标是(m,
),在y=-
x+4中,令y=
,解得:x=3-
,故D的坐标是(3-
,
);
在y=-
x+4中,令x=m,解得:y=4-
m,则C的坐标是:(m,4-
m).
则AD=
=
,
BC=
=
m,
则AD•BC=
•
m=
.
故答案是:5,
.
∴OA=3,OB=4,
∴由勾股定理得AB=
| 32+42 |
(2):设直线AB的解析式是y=kx+b,
则:
|
解得:
则直线的解析式是:y=-
| 4 |
| 3 |
设P的坐标是(m,
| 6 |
| m |
| 4 |
| 3 |
| 6 |
| m |
| 9 |
| 2m |
| 9 |
| 2m |
| 6 |
| m |
在y=-
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
则AD=
(
|
| 15 |
| 2m |
BC=
m2+(
|
| 5 |
| 3 |
则AD•BC=
| 15 |
| 2m |
| 5 |
| 3 |
| 25 |
| 2 |
故答案是:5,
| 25 |
| 2 |
点评:本题考查了待定系数法求函数的解析式,利用数形结合解决此类问题,是非常有效的方法.

练习册系列答案
相关题目
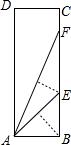 (2013•永春县质检)将如图所示的矩形纸片ABCD沿过点B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,则
(2013•永春县质检)将如图所示的矩形纸片ABCD沿过点B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,则 (2013•永春县质检)已知正比例函数y=x和反比例函数
(2013•永春县质检)已知正比例函数y=x和反比例函数