题目内容
 (2013•永春县质检)已知正比例函数y=x和反比例函数y=
(2013•永春县质检)已知正比例函数y=x和反比例函数y=| k |
| x |
(1)求反比例函数的解析式;
(2)将直线OA绕点O顺时针旋转得到直线l,当直线l过点B(3,
| 3 |
(3)点P在y轴上,若△AOP是等腰三角形,请直接写出P点的坐标.
分析:(1)将A坐标代入反比例解析式求出k的值,确定出反比例函数解析式;
(2)求出直线OA的倾斜角,以及直线l的倾斜角,相减即可求出∠AOB的度数;
(3)以A为圆心,OA长为半径画弧,与y轴交于两点,即为点P;做出选段OA的垂直平分线,与y轴交于P点,写出所有满足题意P的坐标即可.
(2)求出直线OA的倾斜角,以及直线l的倾斜角,相减即可求出∠AOB的度数;
(3)以A为圆心,OA长为半径画弧,与y轴交于两点,即为点P;做出选段OA的垂直平分线,与y轴交于P点,写出所有满足题意P的坐标即可.
解答: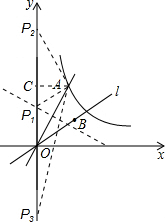 解:(1)将A(3,3)代入反比例函数解析式得:k=9,
解:(1)将A(3,3)代入反比例函数解析式得:k=9,
∴y=
;
(2)∵正比例函数y=x,直线l:y=
x,
∴正比例函数倾斜角为45°,直线l倾斜角为30°,
∴∠AOB=15°;
(3)作出线段OA的垂直平分线,与y轴交于P1点,
∵A(3,3),
∴OA=3
,
∵∠AOP1=45°,
∴OP1=
×
=3,即P1(0,3);
以A为圆心,OA长为半径画弧,与y轴交于两点,即为点P2与P3;,
过A作AC⊥y轴,以y轴交于C点,可得出AC=OC=3,
∴P2C=OC=3,即OP2=6,
∴P2(0,6);
∵OA=OP3=3
,
∴P3(0,-3
).
综上,满足题意P的坐标为(0,3)或(0,6)或(0,-3
).
 解:(1)将A(3,3)代入反比例函数解析式得:k=9,
解:(1)将A(3,3)代入反比例函数解析式得:k=9,∴y=
| 9 |
| x |
(2)∵正比例函数y=x,直线l:y=
| ||
| 3 |
∴正比例函数倾斜角为45°,直线l倾斜角为30°,
∴∠AOB=15°;
(3)作出线段OA的垂直平分线,与y轴交于P1点,
∵A(3,3),
∴OA=3
| 2 |
∵∠AOP1=45°,
∴OP1=
| 2 |
3
| ||
| 2 |
以A为圆心,OA长为半径画弧,与y轴交于两点,即为点P2与P3;,
过A作AC⊥y轴,以y轴交于C点,可得出AC=OC=3,
∴P2C=OC=3,即OP2=6,
∴P2(0,6);
∵OA=OP3=3
| 2 |
∴P3(0,-3
| 2 |
综上,满足题意P的坐标为(0,3)或(0,6)或(0,-3
| 2 |
点评:此题考查了反比例综合题,涉及的知识有:坐标与图形性质,线段垂直平分线,直线的倾斜角,以及待定系数法,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
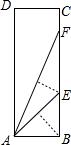 (2013•永春县质检)将如图所示的矩形纸片ABCD沿过点B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,则
(2013•永春县质检)将如图所示的矩形纸片ABCD沿过点B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,则