题目内容
(2013•永春县质检)一个不透明的口袋里装有红、白、黄三种颜色的小球(除颜色外其余都相同),其中白球有2个,黄球有1个.若从中任意摸出一个球,这个球是白球的概率为
.
(1)求口袋中红球的个数;
(2)把口袋中的球搅匀后先摸出一个球,不放回,再摸出第二个球,请你用画树状图或列表的方法表示所有等可能的结果,并说明摸出‘一黄一白’和摸出‘两个白球’这两个事件发生的概率相等吗?为什么?
| 1 | 2 |
(1)求口袋中红球的个数;
(2)把口袋中的球搅匀后先摸出一个球,不放回,再摸出第二个球,请你用画树状图或列表的方法表示所有等可能的结果,并说明摸出‘一黄一白’和摸出‘两个白球’这两个事件发生的概率相等吗?为什么?
分析:(1)设口袋中红球的个数为x,根据题概率公式得到
=
,然后解方程即可;
(2)先利用列表法展示所有6种等可能的结果,其中‘一黄一白’占2种,‘两个白球’占1种,然后根据概率公式分别计算它们的概率即可.
| 2 |
| 2+1+x |
| 1 |
| 2 |
(2)先利用列表法展示所有6种等可能的结果,其中‘一黄一白’占2种,‘两个白球’占1种,然后根据概率公式分别计算它们的概率即可.
解答:解:(1)设口袋中红球的个数为x,根据题意得
=
,
解得x=1,
所以口袋中红球的个数为1个;
(2)列表如下:
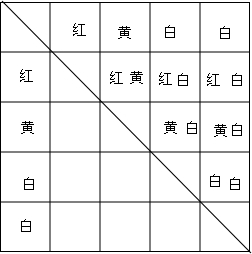
共有6种等可能的结果,其中‘一黄一白’占2种,‘两个白球’占1种,
所以摸出‘一黄一白’的概率=
=
,摸出‘两个白球’的概率=
,
所以摸出‘一黄一白’和摸出‘两个白球’这两个事件发生的概率不相等.
| 2 |
| 2+1+x |
| 1 |
| 2 |
解得x=1,
所以口袋中红球的个数为1个;
(2)列表如下:

共有6种等可能的结果,其中‘一黄一白’占2种,‘两个白球’占1种,
所以摸出‘一黄一白’的概率=
| 2 |
| 6 |
| 1 |
| 3 |
| 1 |
| 6 |
所以摸出‘一黄一白’和摸出‘两个白球’这两个事件发生的概率不相等.
点评:本题考查了列表法与树状图法:先利用列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率的公式计算概率.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
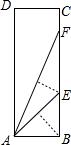 (2013•永春县质检)将如图所示的矩形纸片ABCD沿过点B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,则
(2013•永春县质检)将如图所示的矩形纸片ABCD沿过点B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,则 (2013•永春县质检)已知正比例函数y=x和反比例函数
(2013•永春县质检)已知正比例函数y=x和反比例函数