题目内容
(2013•永春县质检)如图,在矩形OABC中,点A、C的坐标分别是(a,0),(0,
),点D是线段BC上的动点(与B、C不重合),过点D作直线l:y=-
x+b交线段OA于点E.
(1)直接写出矩形OABC的面积(用含a的代数式表示);
(2)已知a=3,当直线l将矩形OABC分成周长相等的两部分时
①求b的值;
②梯形ABDE的内部有一点P,当⊙P与AB、AE、ED都相切时,求⊙P的半径.
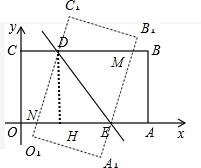
(3)已知a=5,若矩形OABC关于直线DE的对称图形为四边形O1A1B1C1,设CD=k,当k满足什么条件时,使矩形OABC和四边形O1A1B1C1的重叠部分的面积为定值,并求出该定值.
| 3 |
| 3 |
(1)直接写出矩形OABC的面积(用含a的代数式表示);
(2)已知a=3,当直线l将矩形OABC分成周长相等的两部分时
①求b的值;
②梯形ABDE的内部有一点P,当⊙P与AB、AE、ED都相切时,求⊙P的半径.
(3)已知a=5,若矩形OABC关于直线DE的对称图形为四边形O1A1B1C1,设CD=k,当k满足什么条件时,使矩形OABC和四边形O1A1B1C1的重叠部分的面积为定值,并求出该定值.

分析:(1)利用A、C的坐标直接求出OA、OC,利用矩形的面积计算方法求出即可
(2)一条直线可以把矩形分成周长相等的两部分,利用直线l:y=-
x+b表示出D、E两点坐标,①利用CD+OE=DB+EA求出b的值;②根据b的值,求出D、E两点坐标连接BE,找出圆心P,利用切线的性质、锐角三角函数、相似三角形求得半径即可;
(3)根据对称的性质,求出重叠部分为菱形,进一步利用勾股定理解决问题.
(2)一条直线可以把矩形分成周长相等的两部分,利用直线l:y=-
| 3 |
(3)根据对称的性质,求出重叠部分为菱形,进一步利用勾股定理解决问题.
解答:解:(1)∵A、C的坐标分别是(a,0),(0,
),
∴OA=
,OA=a,
则矩形OABC的面积是
a;
(2)①直线l将矩形OABC分成周长相等的两部分,
∴CD+OE=DB+EA,
D(
,
),E(
,0),
∴
=6-
,b=2
;
②D(1,
)、E(2,0),
连接BE,
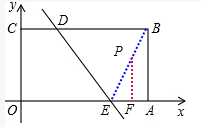
tan∠BEA=tan∠DEO=
,
DEO=60°
∴∠BEA=∠BED,
∵⊙P与AB、AE、ED都相切,
∴圆心P必在BE上,
过P作PF⊥OA,垂足为F,
∴△EPF∽△EBA,
∴
=
,
设⊙P的半径为r,
=
,
∴r=
;
(3)由题意知,DM∥NE,DN∥ME,
∴四边形DNEM为平行四边形,
根据轴对称知,∠MED=∠NED,
又∠MDE=∠NED,
∴∠MED=∠MDE,
∴MD=ME,
∴平行四边形DNEM为菱形.
当N与O重合时,CD=1,
当M与B重合时,CD=3,
∴当1≤k≤3时重叠部分的面积为定值.
过点D作DH⊥OA,垂足为H,
由题意知,tan∠DEN=
,DH=
,
∴HE=1,
设菱形DNEM的边长为a,
则在Rt△DHN中,由勾股定理知,
a2=(a-1)2+(
)2
a=2,
∴S四边形DNEM=NE•DH=2
;
∴该定值为2
.
| 3 |
∴OA=
| 3 |
则矩形OABC的面积是
| 3 |
(2)①直线l将矩形OABC分成周长相等的两部分,
∴CD+OE=DB+EA,
D(
b-
| ||
|
| 3 |
| b | ||
|
∴
2b-
| ||
|
2b-
| ||
|
| 3 |
②D(1,
| 3 |
连接BE,

tan∠BEA=tan∠DEO=
| 3 |
DEO=60°
∴∠BEA=∠BED,
∵⊙P与AB、AE、ED都相切,
∴圆心P必在BE上,
过P作PF⊥OA,垂足为F,
∴△EPF∽△EBA,
∴
| PF |
| BA |
| EF |
| EA |
设⊙P的半径为r,
| r | ||
|
| 1-r |
| 1 |
∴r=
3-
| ||
| 2 |
(3)由题意知,DM∥NE,DN∥ME,
∴四边形DNEM为平行四边形,
根据轴对称知,∠MED=∠NED,
又∠MDE=∠NED,
∴∠MED=∠MDE,
∴MD=ME,
∴平行四边形DNEM为菱形.
当N与O重合时,CD=1,
当M与B重合时,CD=3,
∴当1≤k≤3时重叠部分的面积为定值.
过点D作DH⊥OA,垂足为H,
由题意知,tan∠DEN=
| 3 |
| 3 |
∴HE=1,
设菱形DNEM的边长为a,
则在Rt△DHN中,由勾股定理知,
a2=(a-1)2+(
| 3 |
a=2,
∴S四边形DNEM=NE•DH=2
| 3 |
∴该定值为2
| 3 |

点评:此题综合考查一次函数,三角形相似的判定与性质,菱形的判定与性质,勾股定理等知识点,难度较大.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
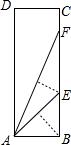 (2013•永春县质检)将如图所示的矩形纸片ABCD沿过点B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,则
(2013•永春县质检)将如图所示的矩形纸片ABCD沿过点B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,则 (2013•永春县质检)已知正比例函数y=x和反比例函数
(2013•永春县质检)已知正比例函数y=x和反比例函数