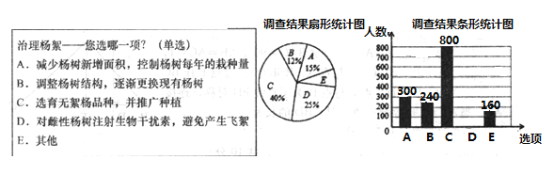
��Ŀ����
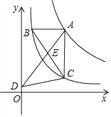
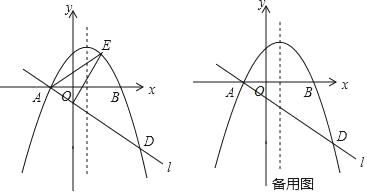
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�������y=ax2��2ax��3a��a��0����x�ύ��A��B���㣨��A�ڵ�B����ࣩ��������A��ֱ��l��y=kx+b��y�Ḻ���ύ�ڵ�C���������ߵ���һ������ΪD����CD=4AC��
��1�������A������͵�D�ĺ����ꣻ
��2����E��ֱ��l�Ϸ����������ϵĶ��㣬����ACE����������ֵΪ![]() ����a��ֵ��
����a��ֵ��
��3����P�������ߵĶԳ����ϵ�һ�㣬��Q���������ϣ��Ե�A��D��P��QΪ������ı����ܷ��Ϊ���Σ����ܣ�ֱ��д����P�����ꣻ�����ܣ���˵�����ɣ�
���𰸡���1��A����1��0������D�ĺ�����Ϊ4����2��a=��![]() ����3����P��1����
����3����P��1����![]() ����1����4����
����1����4����
��������
��1���ⷽ�̼��ɵõ����ۣ�����ֱ��l��y=kx+b��A����1��0�����õ�ֱ��l��y=kx+k��
�ⷽ�̵õ���D�ĺ�����Ϊ4�����k=a���õ�ֱ��l�ĺ�������ʽΪy=ax+a��
��2����E��EF��y�ύֱ��l��F����E��x��ax2��2ax��3a�����õ�F��x��ax+a�������
EF=ax2��3ax��4a�����������ε������ʽ�з��̼��ɵõ����ۣ�
��3����ax2��2ax��3a=ax+a����ax2��3ax��4a=0���õ�D��4��5a������P��1��m��������AD
�Ǿ���ADPQ��һ���ߣ�����AD�Ǿ���APDQ�ĶԽ��ߣ��з��̼��ɵõ����ۣ�
�⣺��1����y=0ʱ��ax2��2ax��3a=0��
��ã�x1=��1��x2=3��
��A����1��0����B��3��0����
��ֱ��l��y=kx+b��A����1��0����
��0=��k+b��
��k=b��
��ֱ��l��y=kx+k��
����������ֱ��l���ڵ�A��D��
��ax2��2ax��3a=kx+k��
��ax2����2a+k��x��3a��k=0��
��CD=4AC��
���D�ĺ�����Ϊ4��
��2���ɣ�1��֪����D�ĺ�����Ϊ4��
![]()
��k=a��
��ֱ��l�ĺ�������ʽΪy=ax+a��
��E��EF��y�ύֱ��l��F����E��x��ax2��2ax��3a����
��F��x��ax+a����EF=ax2��2ax��3a��ax��a=ax2��3ax��4a��
��S��ACE=S��AFE��S��CEF![]() ��
��
![]()
���ACE����������ֵ=![]() ��
��
�ߡ�ACE����������ֵΪ![]() ��
��
��![]()
���![]()
��3���Ե�A��D��P��QΪ������ı����ܳ�Ϊ���Σ�
��ax2��2ax��3a=ax+a����ax2��3ax��4a=0��
��ã�x1=��1��x2=4��
��D��4��5a����
�������ߵĶԳ���Ϊֱ��x=1��
��P��1��m����
����AD�Ǿ���ADPQ��һ���ߣ�
����Q����4��21a����
m=21a+5a=26a����P��1��26a����
���ı���ADPQ�Ǿ��Σ�
���ADP=90�㣬
��AD2+PD2=AP2��
��52+��5a��2+32+��26a��5a��2=22+��26a��2��
��![]()
��a��0��
��![]()
��![]()
����AD�Ǿ���APDQ�ĶԽ��ߣ�
����Q��2����3a����
m=5a������3a��=8a����P��1��8a����
���ı���APDQ�Ǿ��Σ�
���APD=90�㣬
��AP2+PD2=AD2��
������1��1��2+��8a��2+��1��4��2+��8a��5a��2=52+��5a��2��
��![]()
��a��0��
��![]()
��P��1����4����
������������A��D��P��QΪ������ı����ܳ�Ϊ���Σ���![]() ��1����4����
��1����4����