Question

【题目】如图所示，线段EF过平行四边形ABCD的对角线的交点O，交AD于点E，交BC于点F。已知AB＝4，BC＝5，EF＝3,那么四边形EFCD的周长是_____.

Answer 1

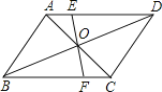
【答案】12

【解析】

根据平行四边形的性质，得△AOE≌△COF．根据全等三角形的性质，得OF=OE，CF=AE．再根据平行四边形的对边相等，得CD=AB，AD=BC，故FC+ED=AE+ED=AD，根据所推出相等关系，可求四边形EFCD的周长．

解：∵四边形ABCD为平行四边形，
∴AO=OC，AD∥BC，
∴∠EAO=∠FCO，
在△AOE和△COF中，

，
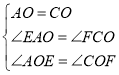∴△AOE≌△COF，
∴OF=OE=1.5，CF=AE，
根据平行四边形的对边相等，得
CD=AB=4，AD=BC=5，
故四边形EFCD的周长=EF+FC+ED+CD=OE+OF+AE+ED+CD=1.5+1.5+5+4=12．
故答案为：12．