题目内容
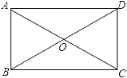
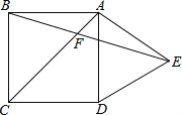
【题目】如图，在正方形ABCD外侧，作等边三角形ADE，AC，BE相交于点F，则∠CBF为（ ）
A.75°B.60°C.55°D.45°
【答案】A
【解析】
根据正方形的性质及等边三角形的性质求出∠ABE=15°，∠BAC=45°，再求∠BFC，进而得出∠CBF．
解：∵四边形ABCD是正方形，
∴AB=AD，
又∵△ADE是等边三角形，
∴AE=AD=DE，∠DAE=60°，
∴AB=AE，
∴∠ABE=∠AEB，∠BAE=90°+60°=150°，
∴∠ABE=（180°-150°）÷2=15°，
又∵∠BAC=45°，
∴∠BFC=45°+15°=60°．
∴∠BFA=180°-60°=120°，
∴∠CBF=180°-∠BCA-∠BFC=180°-45°-60=75°，
故选：A．
练习册系列答案
相关题目
【题目】为了解某校学生的身高情况，王老师随机抽取该校男生、女生进行抽样调查，已知抽取的样本中，男生、女生人数相同，利用所得数据绘制如下统计图表：
组别 | 身高 |
|
|
|
|
|
|
|
|
|
|
身高情况分组表
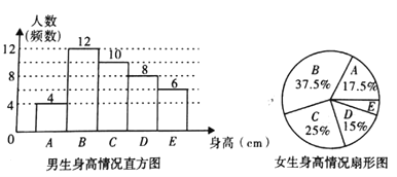
根据图表提供的信息，回答下列问题：
（1）样本中，女生身高在
组的人数有_________人；
（2）在上面的扇形统计图中，表示组的扇形的圆心角是_________°；
（3）已知该校共有男生800人，女生760人，请估计该校身高在
之间的学生约有多少人？