题目内容
【题目】
中，
，
，以
为一边，在
外部作等腰直角三角形
，则线段
的长为_______．
【答案】8或
或
【解析】
存在三种情况，一种是AD=AC，∠DAC=90°，第二种是AC=CD，∠ACD=90°，第三种是AD=DC，∠ADC=90°．第一种直接可得出BD长，后两种构造直角三角形，利用勾股定理可求得BD的长．
情况一：AD=AC，∠DAC=90°，图形如下
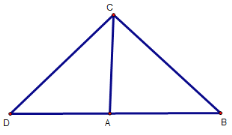
∵AB=AC=4，AC=AD
∴BD=4+4=8
情况二：AC=CD，∠ACD=90°，图形如下，过点D作AB的垂线，交AB反向延长线于点E，连接BD
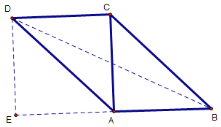
∵AB=AC=4，AC=CD，
∴CD=4
∵∠DCA=90°，∠CAB=90°，∠DEA=90°
∴CD∥AE，DE∥CA，
∴四边形ACDE是平行四边形
∴DE=CA=4，EA=DC=4
在Rt△DEB中，DE=4，EB=8，
∴BD=
情况三：AD=DC，∠ADC=90°，图形如下，过点D作AB的垂线，交AB反向延长线于点E，过点D作AC的垂线，交AC于点F
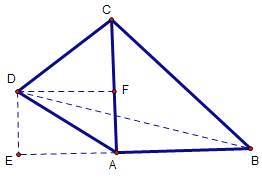
∵AB=AC=4，△ACD是等腰直角三角形，DF⊥AC
∴DF=FA=FC=2
同理，四边形DFAE是平行四边形
∴DE=FA=2，AE=DF=2
在Rt△DEB中，DE=2，EB=6，
∴BD=
故答案为：8或或
练习册系列答案
相关题目
