Question

【题目】已知：在△ABC中，∠BAC＝90°，AB＝AC．

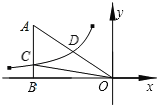
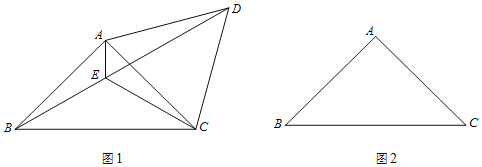
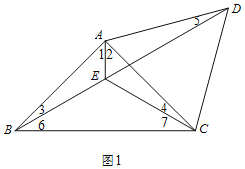
（1）如图1，将线段AC绕点A逆时针旋转60°得到AD，连结CD、BD，∠BAC的平分线交BD于点E，连结CE．

①求证：∠AED＝∠CED；

②用等式表示线段AE、CE、BD之间的数量关系（直接写出结果）；

（2）在图2中，若将线段AC绕点A顺时针旋转60°得到AD，连结CD、BD，∠BAC的平分线交BD的延长线于点E，连结CE．请补全图形，并用等式表示线段AE、CE、BD之间的数量关系，并证明．

Answer 1

【答案】（1）①证明见解析；②BD＝2CE+AE，理由见解析；（2）补图见解析，2CE﹣AE＝BD，证明见解析.

【解析】

(1)①由旋转的性质可得AC=AD,∠DAC=60°,由”SAS”可证△ABE≌ACE,可得∠3=∠4=15°,由三角形外角的性质可得结论;②过点A作AH⊥BD于点H,由等腰三角形的性质和直角三角形性质可得BD=2BH=2(BE+EH)=2BE+AE=2EC+AE;

(2)以A为顶点,AE为一边作∠EAF=60°,AF交DB延长线于点F,通过证明△CAE≌△DAF和△BAE≌△CAE,可得CE=DF,BE=CE,即可得2CE-AE=BD.

证明：（1）

①∵将线段AC绕点A逆时针旋转60°得到AD，

∴AC＝AD，∠DAC＝60°

∴∠BAD＝∠BAC+∠CAD＝150°，且AB＝AC＝AD

∴∠3＝∠5＝15°

∵∠BAC＝90°，AB＝AC，AE平分∠BAC

∴∠1＝∠2＝45°，∠ABC＝∠ACB＝45°

又∵AE＝AE，

∴△ABE≌△ACE（SAS）

∴∠3＝∠4＝15°

∴∠6＝∠7＝30°

∴∠DEC＝∠6+∠7＝60°

∵∠AED＝∠3+∠1＝60°

∴∠AED＝∠CED

②BD＝2CE+AE

理由如下：

过点A作AH⊥BD于点H，

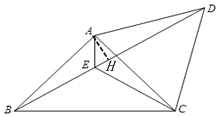
∵∠EBC＝∠ECB

∴BE＝CE，

∵∠AED＝60°，AH⊥BD

∴AE＝2EH

∵AB＝AD，AH⊥BD

∴BD＝2BH＝2（BE+EH）＝2BE+AE＝2EC+AE

（2）补全图形如图，

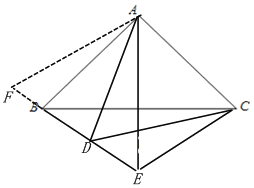
2CE﹣AE＝BD

理由如下：

如图2，以A为顶点，AE为一边作∠EAF＝60°，AF交DB延长线于点F．

∵∠BAC＝90°，AB＝AC，AE平分∠BAC

∴∠BAE＝∠CAE＝45°，∠ABC＝∠ACB＝45°．

∵将线段AC绕点A逆时针旋转60°得到AD，

∴AC＝AD，∠DAC＝60°

∴∠DAE＝∠DAC﹣∠CAE＝15°，AB＝AD

∴∠ABD＝∠ADB，∠BAD＝30°

∴∠ABD＝∠ADB＝75°

∴∠AED＝∠ADB﹣∠DAE＝60°

∵∠EAF＝60°

又∵∠EAF＝60°，

∴∠F＝60°

∴△AEF是等边三角形．

∴AE＝AF＝EF．

∵AC＝AD，∠CAE＝∠DAF＝45°，AE＝AF，

∴△CAE≌△DAF（SAS）．

∴CE＝DF．

∵AB＝AC，∠BAE＝∠CAE＝45°，AE＝AE，

∴△BAE≌△CAE（SAS）．

∴BE＝CE．

∴BE＝CE．

∵DF+BE﹣EF＝BD，

∴2CE﹣AE＝BD