题目内容
【题目】如图所示,一动点从半径为 2 的⊙O上的 A0点出发,沿着射线 A0O 方向运动到⊙O上的点 A1处,再向左沿着与射线 A1O 夹角为60°的方向运动到⊙O上的点 A2处;接着又从 A2点出发,沿着射线 A2O 方向运动到⊙O上的点 A3处,再向左沿着与射线 A3O 夹角为60°的方向运动到⊙O上的点 A4处;…按此规律运动到点 A2017处,则点 A2017与点 A0间的距离是( )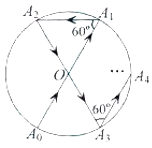
A.4
B.2
C.![]()
D.0
【答案】A
【解析】如图:∵⊙O的半径为2,
∴A0A1=4,
又∵∠OA1A2=60°,OA1=OA2,
∴△OA1A2为等边三角形,
∴A1A2=2,
∴△A0A1A2为直角三角形,
∴A0A2=![]() =2
=2![]() ,
,
结合题意由此规律得出:
A0A3=2,A0A4=2![]() ,A0A5=2,A0A6=0,A0A7=4……
,A0A5=2,A0A6=0,A0A7=4……
又∵2017÷6=336……1
∴按此规律运动到点A2017处,与A1重合,
∴A0A2017=A0A1=4,
所以答案是:A.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目