题目内容
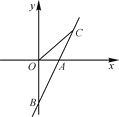
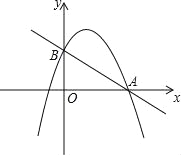
【题目】如图,已知二次函数y1=-x2+![]() x+c的图象与x轴的一个交点为A(4,0),与y轴的交点为B,过A、B的直线为y2=kx+b.
x+c的图象与x轴的一个交点为A(4,0),与y轴的交点为B,过A、B的直线为y2=kx+b.
(1)求二次函数y1的解析式及点B的坐标;
(2)由图象写出满足y1<y2的自变量x的取值范围;
(3)在两坐标轴上是否存在点P,使得△ABP是以AB为底边的等腰三角形?若存在,求出P的坐标;若不存在,说明理由.
【答案】(1)y=-x2+![]() x+3,B点坐标为(0,3);(2) x<0或x>4 (3)P1(0,-
x+3,B点坐标为(0,3);(2) x<0或x>4 (3)P1(0,-![]() ),P2(
),P2(![]() ,0).
,0).
【解析】
试题分析:(1)根据待定系数法,可得函数解析式,根据自变量为零,可得B点坐标;
(2)根据一次函数图象在上方的部分是不等式的解集,可得答案;
(3)根据线段垂直平分线上的点到线段两点间的距离相等,可得P在线段的垂直平分线上,根据直线AB,可得AB的垂直平分线,根据自变量为零,可得P在y轴上,根据函数值为零,可得P在x轴上.
试题解析:(1)将A点坐标代入y1,得
-16+13+c=0.
解得c=3,
二次函数y1的解析式为y=-x2+![]() x+3,
x+3,
B点坐标为(0,3);
(2)由图象得直线在抛物线上方的部分,是x<0或x>4,
∴x<0或x>4时,y1<y2;
(3)直线AB的解析式为y=-![]() x+3,
x+3,
AB的中点为(2,![]() )
)
AB的垂直平分线为y=![]() x-
x-![]()
当x=0时,y=-![]() ,P1(0,-
,P1(0,-![]() ),
),
当y=0时,x=![]() ,P2(
,P2(![]() ,0),
,0),
综上所述:P1(0,-![]() ),P2(
),P2(![]() ,0),使得为底边的等腰三角形.△ABP是以AB
,0),使得为底边的等腰三角形.△ABP是以AB

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目