题目内容
如图，OA=4，线段OA的中点为B，点P在以O为圆心，OB为半径的圆上运动，PA的中点为Q．当点Q也落在⊙O上时，cos∠OQB的值等于（ ）
A．
| B．
| C．
| D．
|
当点P运动到恰好点Q落在⊙O上，连接QB，OP，BC，再连接QO并延长交⊙O于点C，则∠CBQ=90°（直径所对的圆周角是直角）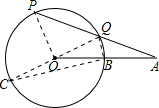
∵B、Q分别是OA、AP的中点，
∴BQ∥OP，
∵OP=OB=BA=
OA=2，
∴QB=1
在Rt△CQB中，∠CBQ=90°
∴cos∠OQB=
=
．
故选C．
∵B、Q分别是OA、AP的中点，
∴BQ∥OP，
∵OP=OB=BA=
| 1 |
| 2 |
∴QB=1
在Rt△CQB中，∠CBQ=90°
∴cos∠OQB=
| QB |
| QC |
| 1 |
| 4 |
故选C．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
