题目内容
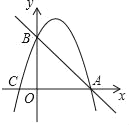
【题目】已知抛物线y=ax2﹣![]() x+c经过A(﹣2,0),B(0,2)两点,动点P,Q同时从原点出发均以1个单位/秒的速度运动,动点P沿x轴正方向运动,动点Q沿y轴正方向运动,连接PQ,设运动时间为t秒
x+c经过A(﹣2,0),B(0,2)两点,动点P,Q同时从原点出发均以1个单位/秒的速度运动,动点P沿x轴正方向运动,动点Q沿y轴正方向运动,连接PQ,设运动时间为t秒
(1)求抛物线的解析式;
(2)当BQ=![]() AP时,求t的值;
AP时,求t的值;
(3)随着点P,Q的运动,抛物线上是否存在点M,使△MPQ为等边三角形?若存在,请求出t的值及相应点M的坐标;若不存在,请说明理由.
【答案】(1)y=-![]() x2-
x2-![]() x+2;(2)当BQ=
x+2;(2)当BQ=![]() AP时,t=1或t=4;(3)存在.当t=
AP时,t=1或t=4;(3)存在.当t=![]() 时,抛物线上存在点M(1,1),或当t=
时,抛物线上存在点M(1,1),或当t=![]() 时,抛物线上存在点M(﹣3,﹣3),使得△MPQ为等边三角形.
时,抛物线上存在点M(﹣3,﹣3),使得△MPQ为等边三角形.
【解析】
(1)把A(﹣2,0),B(0,2)代入y=ax2-![]() x+c,求出解析式即可;
x+c,求出解析式即可;
(2)BQ=![]() AP,要考虑P在OC上及P在OC的延长线上两种情况,有此易得BQ,AP关于t的表示,代入BQ=
AP,要考虑P在OC上及P在OC的延长线上两种情况,有此易得BQ,AP关于t的表示,代入BQ=![]() AP可求t值.
AP可求t值.
(3)考虑等边三角形,我们通常只需明确一边的情况,进而即可描述出整个三角形.考虑△MPQ,发现PQ为一有规律的线段,易得OPQ为等腰直角三角形,但仅因此无法确定PQ运动至何种情形时△MPQ为等边三角形.若退一步考虑等腰,发现,MO应为PQ的垂直平分线,即使△MPQ为等边三角形的M点必属于PQ的垂直平分线与抛物线的交点,但要明确这些交点仅仅满足△MPQ为等腰三角形,不一定为等边三角形.确定是否为等边,我们可以直接由等边性质列出关于t的方程,考虑t的存在性.
(1)∵抛物线经过A(﹣2,0),B(0,2)两点,
∴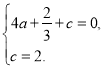 ,解得
,解得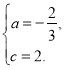
∴抛物线的解析式为y=-![]() x2-
x2-![]() x+2.
x+2.
(2)由题意可知,OQ=OP=t,AP=2+t.
①当t≤2时,点Q在点B下方,此时BQ=2-t.
∵BQ=![]() AP,∴2﹣t=
AP,∴2﹣t=![]() (2+t),∴t=1.
(2+t),∴t=1.
②当t>2时,点Q在点B上方,此时BQ=t﹣2.
∵BQ=![]() AP,∴t﹣2=
AP,∴t﹣2=![]() (2+t),∴t=4.
(2+t),∴t=4.
∴当BQ=![]() AP时,t=1或t=4.
AP时,t=1或t=4.
(3)存在.
作MC⊥x轴于点C,连接OM.
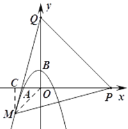
设点M的横坐标为m,则点M的纵坐标为-![]() m2-
m2-![]() m+2.
m+2.
当△MPQ为等边三角形时,MQ=MP,
又∵OP=OQ,
∴点M点必在PQ的垂直平分线上,
∴∠POM=![]() ∠POQ=45°,
∠POQ=45°,
∴△MCO为等腰直角三角形,CM=CO,
∴m=-![]() m2-
m2-![]() m+2,
m+2,
解得m1=1,m2=﹣3.
∴M点可能为(1,1)或(﹣3,﹣3).
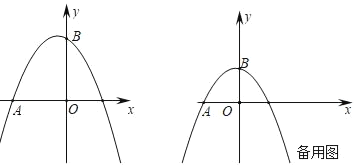
①如图,
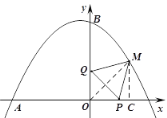
当M的坐标为(1,1)时,
则有PC=1﹣t,MP2=1+(1﹣t)2=t2﹣2t+2,
PQ2=2t2,
∵△MPQ为等边三角形,
∴MP=PQ,
∴t2﹣2t+2=2t2,
解得t1=![]() ,t2=
,t2=![]() (负值舍去).
(负值舍去).
②如图,
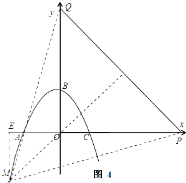
当M的坐标为(﹣3,﹣3)时,
则有PC=3+t,MC=3,
∴MP2=32+(3+t)2=t2+6t+18,PQ2=2t2,
∵△MPQ为等边三角形,
∴MP=PQ,
∴t2+6t+18=2t2,
解得t1=![]() ,t2=
,t2=![]() (负值舍去).
(负值舍去).
∴当t=![]() 时,抛物线上存在点M(1,1),或当t=
时,抛物线上存在点M(1,1),或当t=![]() 时,抛物线上存在点M(﹣3,﹣3),使得△MPQ为等边三角形.
时,抛物线上存在点M(﹣3,﹣3),使得△MPQ为等边三角形.

【题目】某品牌手机去年每台的售价y(元)与月份x之间满足函数关系:y=﹣50x+2600,去年的月销量p(万台)与月份x之间成一次函数关系,其中1﹣6月份的销售情况如下表:
月份(x) | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 |
销售量(p) | 3.9万台 | 4.0万台 | 4.1万台 | 4.2万台 | 4.3万台 | 4.4万台 |
(1)求p关于x的函数关系式;
(2)求该品牌手机在去年哪个月的销售金额最大?最大是多少万元?
(3)今年1月份该品牌手机的售价比去年12月份下降了m%,而销售量也比去年12月份下降了1.5m%.今年2月份,经销商决定对该手机以1月份价格的“八折”销售,这样2月份的销售量比今年1月份增加了1.5万台.若今年2月份这种品牌手机的销售额为6400万元,求m的值.