题目内容
【题目】如图,在平面直角坐标系中,等边△ABC的顶点B,C的坐标分别为(2,0),(6,0),点N从A点出发沿AC向C点运动,连接ON交AB于点M,当点M恰平分线段ON时,求线段CN的长. 
【答案】解:作ND∥AB交OC于D,如图所示: 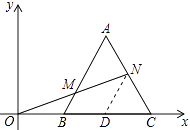
则∠NDC=∠ABC,∠DNC=∠A,
∵OM=MN,
∴OB=BD,
∵点B、C的坐标分别为(2,0),(6,0),
∴OB=2,OB=6,
∴BC=4,BD=OB=2,
∴BD=CD=2,
∵△ABC是等边三角形,
∴∠A=∠ABC=∠ACB=60°,AC=BC=4,
∴∠DNC=∠NDC=∠AC60°,
∴△CDN是等边三角形,
∴CN=DN=CD=2.
【解析】作ND∥AB交OC于D,则∠NDC=∠ABC,∠DNC=∠A,由点的坐标得出OB=2,OB=6,得出BC=4,BD=CD=2,由等边三角形的性质得出∠A=∠ABC=∠ACB=60°,AC=BC=4,证明△CDN是等边三角形,得出CN=DN=CD=2.
【考点精析】掌握等边三角形的性质是解答本题的根本,需要知道等边三角形的三个角都相等并且每个角都是60°.

练习册系列答案
相关题目