题目内容
【题目】如图,四边形ABCD中,AB=BC=2CD,AB∥CD,∠C=90°,E是BC的中点,AE与BD相交于点F,连接DE
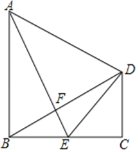
(1)求证:△ABE≌△BCD;(2)若CD=1,试求△AED的面积.
【答案】(1)见解析;(2)1.5.
【解析】
(1)先根据已知条件和中点定义证出:BE=CD,然后根据平行线的性质证出:∠ABE=∠C,最后利用SAS即可证出:△ABE≌△BCD;
(2)根据S△AED=S梯形ABCD-S△ABE-S△DCE计算即可.
证明:(1)∵AB=BC=2CD,E是BC的中点,
∴BE=CE=![]() BC,CD=
BC,CD=![]() BC,
BC,
∴BE=CD
∵AB∥CD,∠C=90°,
∴∠ABE=180°-∠C=90°,
∴∠ABE=∠C
在△ABE和△BCD中
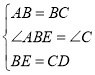
∴△ABE≌△BCD;
解:(2)∵AB=BC=2CD,CD=1,
∴AB=BC=2,BE=CE=1
∴S△AED=S梯形ABCD-S△ABE-S△DCE
=![]() BC·(AB+CD)-
BC·(AB+CD)-![]() BE·AB-
BE·AB-![]() CE·DC
CE·DC
=![]() ×2×(2+1)-
×2×(2+1)-![]() ×1×2-
×1×2-![]() ×1×1
×1×1
=1.5

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目