题目内容
【题目】在平面直角坐标系中,点![]() ,
,![]() .
.
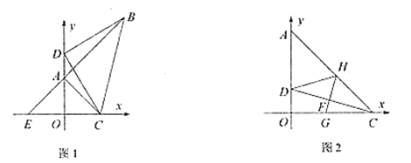
(1)若![]() ,
,![]() 满足
满足![]() .
.
①直接写出![]() ______,
______,![]() ______.
______.
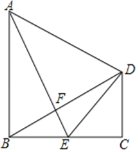
②如图1,![]() 为点
为点![]() 上方一点,连接
上方一点,连接![]() ,在
,在![]() 轴右侧作等腰
轴右侧作等腰![]() ,
,![]() ,连接
,连接![]() 并延长交
并延长交![]() 轴于点
轴于点![]() ,当点
,当点![]() 上方运动时,求
上方运动时,求![]() 的面积;
的面积;
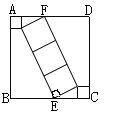
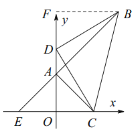
(2)如图2,若![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() ,
,![]() 为
为![]() 上一点,且
上一点,且![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .连接
.连接![]() ,当
,当![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)①![]() ;②16;(2)
;②16;(2)![]() .
.
【解析】
(1)①解方程组求出m,n即可.
②过点![]() 作
作![]() 轴于点
轴于点![]() ,设
,设![]() ,证明
,证明![]() ,可得BF=OD,FD=OC,用t表示OD,AF,BF,得出AF=BF,根据等腰三角形的判定得
,可得BF=OD,FD=OC,用t表示OD,AF,BF,得出AF=BF,根据等腰三角形的判定得![]() 是等腰直角三角形,再由平行线的性质得出
是等腰直角三角形,再由平行线的性质得出![]() 是等腰直角三角形,则EO=OC=AO=4,由此即可解决问题.
是等腰直角三角形,则EO=OC=AO=4,由此即可解决问题.
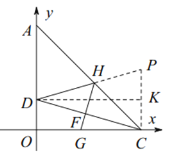
(2)如图2中,作CP∥OA交DH的延长线于P,作DK⊥CP于K.证明△HCG≌△HCP(AAS),推出CG=CP,由此构建方程即可解决问题.
解:(1)①![]() ,解得
,解得![]() ,
,
故答案为:![]() ;
;
②过点![]() 作
作![]() 轴于点
轴于点![]() ,设
,设![]() ,
,
∴∠BFD=∠DOC=90°,∠BDF+∠DBF=90°,
∵![]() ,
,
∴∠BDF+∠CDO=90°,
∴∠CDO=∠DBF,
∵等腰![]() ,
,
∴DB=CD,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 是等腰直角三角形,∠FBA=45°,
是等腰直角三角形,∠FBA=45°,
∵![]()
∴BF∥x轴,
∴∠OEA=∠FBA=45°,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴EO=OC=AO=4,,
∴![]() 的面积为:
的面积为:![]() =16;
=16;
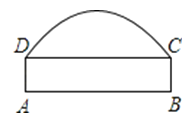
(2)作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,
则![]() ,
,![]() ,
,
又![]() ,
,
∴![]() ,
,
∴![]() 是等腰三角形.
是等腰三角形.
作![]() 于点
于点![]() ,则
,则![]() ,
,
由平移可得![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
∵∠CGH+∠OCD=90°,∠ODC+∠OCD=90°,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴∠CGH=∠P,
∵![]() ,
,![]() ,
,
∴∠GCH=∠OAC =∠PCH,
又∵CH=CH
∴![]() ,
,
∴![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目