��Ŀ����
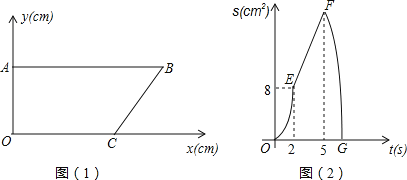
����Ŀ����ͼ(1)����ƽ��ֱ������ϵ�У���A��C�ֱ���y���x���ϣ�AB��x�ᣬcosB��![]() ����P��B���������1cm/s���ٶ��ر�BA�����˶�����Q�ӵ�A���������߶�AO��OC��CB�����˶�����P���Qͬʱ����������һ�㵽���յ㣬��һ��Ҳ��ֹ֮ͣ�˶������P�˶���ʱ��Ϊt(s)����BPQ�����ΪS(cm2)�� ��֪S��t֮��ĺ�����ϵ��ͼ(2)�е����߶�OE���߶�EF�����߶�FG��
����P��B���������1cm/s���ٶ��ر�BA�����˶�����Q�ӵ�A���������߶�AO��OC��CB�����˶�����P���Qͬʱ����������һ�㵽���յ㣬��һ��Ҳ��ֹ֮ͣ�˶������P�˶���ʱ��Ϊt(s)����BPQ�����ΪS(cm2)�� ��֪S��t֮��ĺ�����ϵ��ͼ(2)�е����߶�OE���߶�EF�����߶�FG��
��1����Q���˶��ٶ�Ϊ cm/s����B������Ϊ ��
��2��������FG�εĺ�������ʽ��
��3����tΪ��ֵʱ����BPQ��������ı���OABC�������![]() ��
��
���𰸡���1��4,(18,8)��
��2������FG�εĺ�������ʽΪ��S=![]() t2+12t��
t2+12t��
��3��t=3��t=![]() ,��BPQ��������ı���OABC�������
,��BPQ��������ı���OABC�������![]() .
.
�������������������1����Ϻ���ͼ��ó���2��ʱ��BP=2����ʱ��BPQ�����Ϊ8cm2���������AOΪ8cm�����ɵó�Q����ٶȣ��������AB�ij����ɣ���2�����ȵó�PB=t��BQ=30-4t����QM=![]() ��30-4t��=24-
��30-4t��=24-![]() t������S��PBQ=
t������S��PBQ=![]() t��24-
t��24-![]() t��������ɣ���3�����ȵó���BPQ������������ó�F�����꣬�����ó�ֱ��EF����ʽΪ��S=4t����S=12ʱ�����t��ֵ���ٽ�S=12����S=-
t��������ɣ���3�����ȵó���BPQ������������ó�F�����꣬�����ó�ֱ��EF����ʽΪ��S=4t����S=12ʱ�����t��ֵ���ٽ�S=12����S=-![]() t2+12t���t��ֵ�����ɵó��𰸣�
t2+12t���t��ֵ�����ɵó��𰸣�
���������(1)������ɵó�����2��ʱ����BPQ������ĺ�����ϵʽ�ı䣬��Q��AO���˶�2�룬
��2��ʱ��BP=2����ʱ��BPQ�����Ϊ8cm2��
��AOΪ8cm��
���Q���˶��ٶ�Ϊ��8��2=4(cm/s)��
���˶���5��ʱ��������ϵʽ�ı䣬��CO=12cm��
��cosB=![]() ��
��
������AB=6+12=18(cm)��
��B(18,8)��
�ʴ�Ϊ��4��(18��8)��
(2)��ͼ(1)��

PB=t��BQ=304t��
����Q��QM��AB�ڵ�M��
��QM=![]() (304t)=24
(304t)=24![]() t��
t��
��S��PBQ=![]() t(24
t(24![]() t)=
t)= ![]() t2+12t(5t7.5)��
t2+12t(5t7.5)��
������FG�εĺ�������ʽΪ��S= ![]() t2+12t��
t2+12t��
(3)��S����OABC=![]() (12+18)��8=120��
(12+18)��8=120��
��![]() ��120=12��
��120=12��
��t>2ʱ��F(5��20)��
��ֱ��EF����ʽΪ��S=4t����S=12ʱ��4t=12����ã�t=3��
��S=12����S=![]() t2+12t��
t2+12t��
��ã�t=![]() ��
��
��5t7.5����t=![]() ��
��
����������t=3��t=![]() ����BPQ��������ı���OABC�������
����BPQ��������ı���OABC�������![]() .
.

 Ӧ�����������Ĵ���ѧ������ϵ�д�
Ӧ�����������Ĵ���ѧ������ϵ�д�