Question

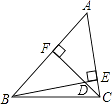
【题目】如图，在平行四边形中，以点为圆心， 为半径的圆，交于点．

(1)求证： ≌；

(2)如果， ， ，求的长．

Answer 1

【答案】（1）证明见解析；（2）EC=.

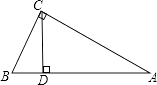
【解析】试题分析：（1）根据平行四边形的性质得出AD=BC，根据圆的半径相等可得出AB=AE，结合等腰三角形的性质和平行线的性质可得出∠B=∠EAD，从而利用SAS可证得结论；（2）在RT△ABC中，可求出BC，过圆心A作AH⊥BC，垂足为H，则BH=HE，则结合cos∠B的值，可求出BH、EH的长度，继而根据EC=BC-BE即可得出答案．

试题解析：(1)∵四边形ABCD是平行四边形，

∴AD=BC，AD∥BC，

∴∠AEB=∠EAD，

∵AB=AE(AB与AE为圆的半径)，

∴∠AEB=∠B，

∴∠B=∠EAD，

在△ABC和△EAD中, ，

故可得△ABC≌△EAD.

(2)∵AB⊥AC，

∴∠BAC=90°，

在Rt△ABC中,cos∠B=，

又∵cos∠B=，AB=6，

∴BC=10，

过圆心A作AH⊥BC，垂足为H，

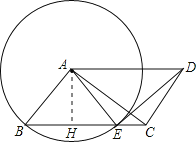
则BH=HE，

在Rt△ABH中,cos∠B=，

则可得，

解得：BH=，

∴BE=，

故可得EC=BCBE=.