题目内容
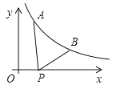
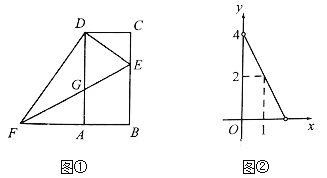
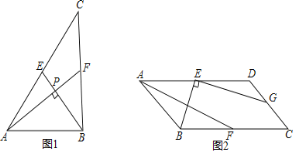
【题目】如图1,AF,BE是△ABC的中线,AF⊥BE,垂足为点P,设BC=a,AC=b,AB=c,则a2+b2=5c2,利用这一性质计算.如图2,在平行四边形ABCD中,E,F,G分别是AD,BC,CD的中点,EB⊥EG于点E,AD=8,AB=2![]() ,则AF=__.
,则AF=__.
【答案】![]()
【解析】
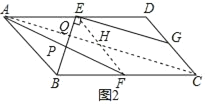
连接AC,EF交于H,AC与BE交于点Q,设BE与AF的交点为P,由点E、G分别是AD,CD的中点,得到EG是△ACD的中位线于是证出BE⊥AC,由四边形ABCD是平行四边形,得到AD∥BC,根据E,F分别是AD,BC的中点,得到![]() ,证出四边形ABFE是平行四边形,证得EH=FH,推出EH,AH分别是△AFE的中线,由题目中的结论得即可得到结果.
,证出四边形ABFE是平行四边形,证得EH=FH,推出EH,AH分别是△AFE的中线,由题目中的结论得即可得到结果.
解:如图2,连接AC,EF交于H,AC与BE交于点Q,设BE与AF的交点为P,
∵点E、G分别是AD,CD的中点,
∴EG∥AC,
∵BE⊥EG,
∴BE⊥AC,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=8,
∴∠EAH=∠FCH,
∵E,F分别是AD,BC的中点,
∴![]()
∴![]()
∵AE∥BF,
∴四边形ABFE是平行四边形,
∴![]()
在△AEH和△CFH中, 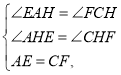
∴△AEH≌△CFH(AAS),
∴EH=FH,
∴EP,AH分别是△AFE的中线,
由a2+b2=5c2得:AF2+EF2=5AE2,
∴![]()
∴![]()
故答案为:![]()

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目