题目内容
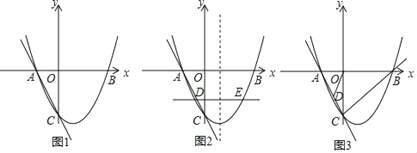
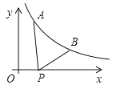
【题目】如图，已知
，
为反比例函数
图象上的两点，动点
在
轴正半轴上运动，当线段
与线段
之差达到最大时，点
的坐标是（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】
求出AB的坐标，设直线AB的解析式是y=kx+b，把A、B的坐标代入求出直线AB的解析式，根据三角形的三边关系定理得出在△ABP中，|AP-BP|＜AB，延长AB交x轴于P′，当P在P′点时，PA-PB=AB，此时线段AP与线段BP之差达到最大，求出直线AB于x轴的交点坐标即可．
把
，
代入反比例函数
，得：
，
，
，
在
中，由三角形的三边关系定理得：
，
延长
交
轴于
，当
在点时，
，
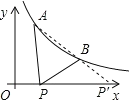
即此时线段
与线段
之差达到最大，
设直线的解析式是
，
把
，
的坐标代入得：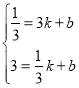
，
解得：
，
直线的解析式是
，
当
时，
，即
，
故选D.
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
【题目】立定跳远是体育中考选考项目之一，体育课上老师记录了某同学的一组立定跳远成绩如表：
成绩（m） | 2.3 | 2.4 | 2.5 | 2.4 | 2.4 |
则下列关于这组数据的说法，正确的是（ ）
A.众数是2.3B.平均数是2.4
C.中位数是2.5D.方差是0.01
【题目】从甲、乙两位运动员中选出一名参加在规定时间内的投篮比赛．预先对这两名运动员进行了6次测试，成绩如下（单位：个）：
甲：6，12，8，12，10，12；
乙：9，10，11，10，12，8；
（1）填表：
平均数 | 众数 | 方差 | |
甲 | 10 |
|
|
乙 |
| 10 |
|
（2）根据测试成绩，请你运用所学的统计知识作出分析，派哪一位运动员参赛更好？为什么？
