题目内容
【题目】如图,线段AB=10,点P在线段AB上,在AB的同侧分别以AP,BP为边长作正方形APCD和BPEF,点M、N分别是EF、CD的中点,则MN的最小值是 . 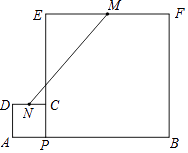
【答案】5
【解析】解:作MG⊥DC于G,如图所示:
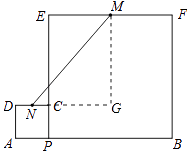
设MN=y,PC=x,
根据题意得:GN=5,MG=|10﹣2x|,
在Rt△MNG中,由勾股定理得:MN2=MG2+GN2,
即y2=52+(10﹣2x)2.
∵0<x<10,
∴当10﹣2x=0,即x=5时,y2最小值=25,
∴y最小值=5.即MN的最小值为5;
所以答案是:5.
【考点精析】根据题目的已知条件,利用二次函数的最值和勾股定理的概念的相关知识可以得到问题的答案,需要掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
【题目】已知某品牌的饮料有大瓶装与小瓶装之分.某超市花了3800元购进一批该品牌的饮料共1000瓶,其中大瓶和小瓶饮料的进价及售价如下表所示:
大瓶 | 小瓶 | |
进价(元/瓶) | 5 | 2 |
售价(元/瓶) | 7 | 3 |
(1)该超市购进大瓶和小瓶饮料各多少瓶?
(2)在大瓶饮料售出200瓶,小瓶饮料售出100瓶后,商家决定将剩下的小瓶饮料的售价降低0.5元销售,并把其中一定数量的小瓶饮料作为赠品,在顾客一次性购买大瓶饮料时,每满2瓶就送1瓶小瓶饮料,送完即止.超市要使这批饮料售完后获得的利润不低于1250元,那么小瓶饮料作为赠品最多只能送出多少瓶?





