题目内容
 如图,已知反比例函数y=
如图,已知反比例函数y=| 12 | x |
(1)求这个一次函数的解析式;
(2)如果等腰梯形ABCD的顶点A、B在这个一次函数的图象上,顶点C、D在这个反比例函数的图象上,两底AD、BC与y轴平行,且A和B的横坐标分别为a、b(b>a>0),求代数式ab的值.
分析:(1)先把P点坐标代入反比例函数解析式求出m,确定P点坐标,然后把P点坐标再代入一次函数解析式求出k的值即可;
(2)作BE⊥AD于E,CF⊥AD于F,根据等腰梯形的性质得到DF=AE;由于A(a,
a-7),B(b,
b-7),则AE=
b-
a;根据两底AD、BC与y轴平行,则D(a,
),C(b,
),所以DF=
-
,于是可得到
b-
a=
-
,然后化简即可得到ab的值.
(2)作BE⊥AD于E,CF⊥AD于F,根据等腰梯形的性质得到DF=AE;由于A(a,
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 12 |
| a |
| 12 |
| b |
| 12 |
| a |
| 12 |
| b |
| 3 |
| 2 |
| 3 |
| 2 |
| 12 |
| a |
| 12 |
| b |
解答:解:(1)把P(m,2)代入y=
得2m=12,解得m=6,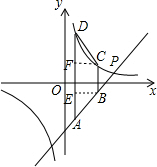
∴P点坐标为(6,2),
把P(6,2)代入y=kx-7得2=6k-7,解得k=
,
∴一次函数的解析式为y=
x-7;
(2)作BE⊥AD于E,CF⊥AD于F,如图,
∵四边形ABCD为等腰梯形ABCD,
∴DF=AE,
∵A和B的横坐标分别为a、b(b>a>0),
∴A(a,
a-7),B(b,
b-7),
∴AE=
b-7-(
a-7)=
b-
a;
∵两底AD、BC与y轴平行,
∴D和C的横坐标分别为a、b,
∴D(a,
),C(b,
),
∴DF=
-
,
∴
b-
a=
-
,
∴ab=8.
| 12 |
| x |

∴P点坐标为(6,2),
把P(6,2)代入y=kx-7得2=6k-7,解得k=
| 3 |
| 2 |
∴一次函数的解析式为y=
| 3 |
| 2 |
(2)作BE⊥AD于E,CF⊥AD于F,如图,
∵四边形ABCD为等腰梯形ABCD,
∴DF=AE,
∵A和B的横坐标分别为a、b(b>a>0),
∴A(a,
| 3 |
| 2 |
| 3 |
| 2 |
∴AE=
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
∵两底AD、BC与y轴平行,
∴D和C的横坐标分别为a、b,
∴D(a,
| 12 |
| a |
| 12 |
| b |
∴DF=
| 12 |
| a |
| 12 |
| b |
∴
| 3 |
| 2 |
| 3 |
| 2 |
| 12 |
| a |
| 12 |
| b |
∴ab=8.
点评:本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征;会利用点的坐标表示线段长;熟练掌握等腰梯形的性质.

练习册系列答案
相关题目
 如图,已知反比例函数
如图,已知反比例函数 如图,已知反比例函数
如图,已知反比例函数 如图,已知反比例函数y=
如图,已知反比例函数y= 如图,已知反比例函数
如图,已知反比例函数 如图,已知反比例函数y=
如图,已知反比例函数y=