题目内容
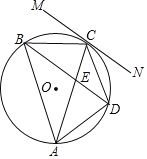
【题目】如图所示,以![]() 的边
的边![]() 为直径作
为直径作![]() ,点
,点![]() 在
在![]() 上,
上,![]() 是
是![]() 的弦,
的弦,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
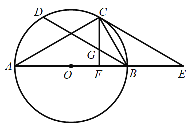
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)求证:![]() ;
;
(3)若![]() ,CG=4,求
,CG=4,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】
(1)连接OC,先证得![]() ,根据垂径定理得到OC⊥BD,根据CE//BD推出OC⊥CE,即可得到结论.
,根据垂径定理得到OC⊥BD,根据CE//BD推出OC⊥CE,即可得到结论.
(2)根据圆周角定理得出∠ACB=90°,然后根据同角的余角相等得出∠A=∠BCF,即可证得∠BCF=∠CBD,根据同角对等边即可证得结论.
(3)连接AD,根据圆周角定理得出∠ADB=90°,即可求得∠BAD=60°,根据圆周角定理得出∠DAC=∠BAC=30°,解直角三角形求得![]() ,然后根据三角形相似和等腰三角形的判定即可求得BE的值.
,然后根据三角形相似和等腰三角形的判定即可求得BE的值.
(1)连接OC
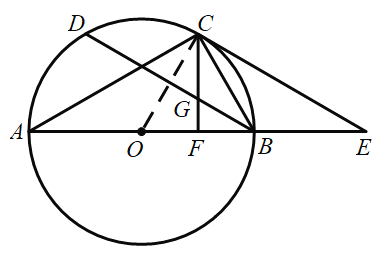
∵∠A=∠CBD
∴![]()
∴OC⊥BD
∵CE//BD
∴OC⊥CE
∴CE是⊙O的切线
(2)∵AB为直径
∴∠ACB=90°
∵CF⊥AB
∴∠ACB=∠CFB=90°
∵∠ABC=∠CBF
∴∠A=∠BCF
∵∠A=∠CBD
∴∠BCF=∠CBD
∴CG=BG
(3)连接AD,

∵AB为直径
∴∠ADB=90°
∵∠DBA=30°
∴∠BAD=60°
∵![]()
∴∠DAC=∠BAC=![]() ∠BAD=30°
∠BAD=30°
∴![]()
∵CE//BD,
∴∠E=∠DBA=30°
∴AC=CE,
∴![]()
∵∠BAC =∠BCF=∠CBD=30°
∴∠BCE=30°
∴BE=BC,
∴△CGB∽△CBE,
∴![]()
∵CG=4,
∴BC=![]()
∴BE=![]()
故答案为:![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目