题目内容
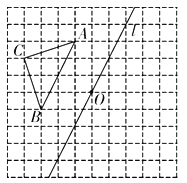
【题目】如图,已知直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,
两点,![]() 是以
是以![]() 为圆心,1为半径的圆上一动点,连接
为圆心,1为半径的圆上一动点,连接![]() 、
、![]() ,当
,当![]() 的面积最大时,点
的面积最大时,点![]() 的坐标为_______.
的坐标为_______.
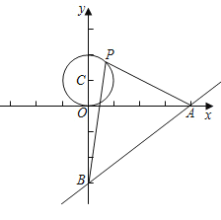
【答案】(![]() ,
,![]() )
)
【解析】
过C作CM⊥AB于M,交x轴于E,连接AC,MC的延长线交⊙C于D,作DN⊥x轴于N,则由三角形面积公式得,![]() ×AB×CM=
×AB×CM=![]() ×OA×BC,可知圆C上点到直线y=
×OA×BC,可知圆C上点到直线y=![]() x-3的最长距离是DM,当P点在D这个位置时,△PAB的面积最大,先证得△COE∽△CMB,求得OE、CE,再通过证得△COE∽△DNE,求得DN和NE,由此求得答案.
x-3的最长距离是DM,当P点在D这个位置时,△PAB的面积最大,先证得△COE∽△CMB,求得OE、CE,再通过证得△COE∽△DNE,求得DN和NE,由此求得答案.
过C作CM⊥AB于M,交x轴于E,连接AC,MC的延长线交⊙C于D,作DN⊥x轴于N,
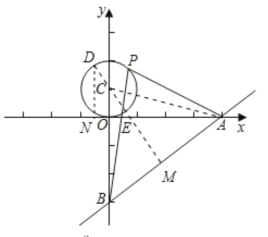
∵直线![]() 与x轴、y轴分别交于A,B两点,
与x轴、y轴分别交于A,B两点,
令x=0,得y=-3,
令y=9,得x=4
∴A(4,0),B(0,3),
∴OA=4,OB=3,
∴AB=![]()
则由三角形面积公式得,![]() ×AB×CM=
×AB×CM=![]() ×OA×BC,
×OA×BC,
∴![]() ×5×CM=
×5×CM=![]() ×4×(1+3),
×4×(1+3),
∴CM=![]()
∴BM=![]()
∴圆C上点到直线![]() 的最大距离是DM=1+
的最大距离是DM=1+![]() =
=![]()
当P点在D这个位置时,△PAB的面积最大,
∵∠CMB=∠COE=90°,∠OCE=∠MCB,
∴△COE∽△CMB,
∴![]()
∴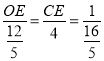
∴OE=,CE=![]() ,
,
∴ED=1+![]() =
=![]()
∵DN⊥x轴,
∴DN∥OC,
∴△COE∽△DNE,
∴![]() ,即
,即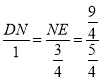
∴DN=![]() ,NE=
,NE=![]()
∴ON=NEOE=![]()
![]() =
=![]()
∴D(![]() ,
,![]() )
)
∴当△PAB的面积最大时,点P的坐标为(![]() ,
,![]() )
)
故答案为:(![]() ,
,![]() )
)

练习册系列答案
相关题目