题目内容
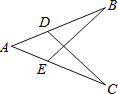
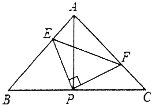
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出下列四个结论:
①AE=CF;
②△EPF是等腰直角三角形;
③EF=AB;
④![]() ,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),上述结论中始终正确的有________(把你认为正确的结论的序号都填上).
,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),上述结论中始终正确的有________(把你认为正确的结论的序号都填上).
【答案】①②④
【解析】
试题∵∠APE、∠CPF都是∠APF的余角,
∴∠APE=∠CPF,
∵AB=AC,∠BAC=90°,P是BC中点,
∴AP=CP,
∴∠PAE=∠PCF,
在△APE与△CPF中,
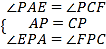 ,
,
∴△APE≌△CPF(ASA),
同理可证△APF≌△BPE,
∴AE=CF,△EPF是等腰直角三角形,S四边形AEPF=![]() S△ABC,①②④正确;
S△ABC,①②④正确;
而AP=![]() BC,当EF不是△ABC的中位线时,则EF不等于BC的一半,EF=AP,
BC,当EF不是△ABC的中位线时,则EF不等于BC的一半,EF=AP,
∴故③不成立.
故始终正确的是①②④.
故选D.

 名校课堂系列答案
名校课堂系列答案【题目】“立定跳远”是我市初中毕业生体育测试项目之一.测试时,记录下学生立定跳远的成绩,然后按照评分标准转化为相应的分数,满分10分.其中男生立定跳远的评分标准如下:注:成绩栏里的每个范围,含最低值,不含最高值.
成绩(米) | … | 1.80~1.86 | 1.86~1.94 | 1.94~2.02 | 2.02~2.18 | 2.18~2.34 | 2.34~ |
得分(分) | … | 5 | 6 | 7 | 8 | 9 | 10 |
某校九年级有480名男生参加立定跳远测试,现从中随机抽取10名男生测试成绩(单位:分)如下:
1.96 2.38 2.56 2.04 2.34 2.17 2.60 2.26 1.87 2.32
请完成下列问题:
(1)求这10名男生立定跳远成绩的极差和平均数;
(2)求这10名男生立定跳远得分的中位数和众数;
(3)如果将9分(含9分)以上定为“优秀”,请你估计这480名男生中得优秀的人数.