题目内容
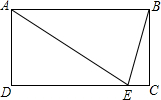
已知矩形ABCD中，AB=3，BC=4，将矩形折叠，使点C与点A重合，则折痕EF的长为______．
连接AC，作AC的中垂线交AD、BC于E、F，设EF与AC交于O点，
易证△AOE≌△COF，得AE=CF，而AD=BC，故DE=BF，
由此可得EF为折痕，连接CE，AE=CE，可得CE=CF．
设CE=CF=x，则BF=4-x，在Rt△CED中，CD=3，DE=BF=4-x，CE=x，
由CD2+DE2=CE2知，x2=9+（4-x）2，故x=
；
过E点作BC边垂线交BC于点G，
在Rt△EGF中，EG=3，FG=4-2BF=
，
故EF=
=
=
．
故答案为：
．
易证△AOE≌△COF，得AE=CF，而AD=BC，故DE=BF，
由此可得EF为折痕，连接CE，AE=CE，可得CE=CF．
设CE=CF=x，则BF=4-x，在Rt△CED中，CD=3，DE=BF=4-x，CE=x，
由CD2+DE2=CE2知，x2=9+（4-x）2，故x=
| 25 |
| 8 |
过E点作BC边垂线交BC于点G，
在Rt△EGF中，EG=3，FG=4-2BF=
| 9 |
| 4 |
故EF=
| EG2+FG2 |
9+
|
| 15 |
| 4 |
故答案为：
| 15 |
| 4 |
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
AB=
