题目内容
平行四边形的四个内角平分线能够围成（ ）
| A．平行四边形 | B．菱形 | C．矩形 | D．正方形 |
如图，在平行四边形ABCD中，∠ABC+∠BAD=180°，
∵AE平分∠BAD，BE平分∠ABC，
∴∠BAE+∠ABE=
（∠BAD+∠ABC）=
×180°=90°，
∴∠AEB=180°-90°=90°，
∴∠1=∠AEB=90°（对顶角相等），
同理∠EFG=∠FGH=∠GHE=90°，
∴四边形EFGH是矩形．
故选C．
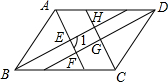
∵AE平分∠BAD，BE平分∠ABC，
∴∠BAE+∠ABE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠AEB=180°-90°=90°，
∴∠1=∠AEB=90°（对顶角相等），
同理∠EFG=∠FGH=∠GHE=90°，
∴四边形EFGH是矩形．
故选C．
练习册系列答案
智慧小复习系列答案
相关题目
