题目内容
【题目】如图,一块四边形草地ABCD,其中∠B=90°,AB=4m,BC=3m,AD=12m,CD=13cm,求这块草地的面积.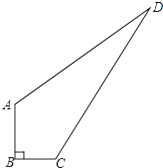
【答案】解:连结AC, 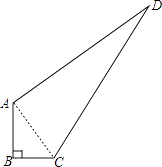
在△ABC中,
∵∠B=90°,AB=4m,BC=3m,
∴AC= ![]() =5(m),
=5(m),
S△ABC= ![]() ×3×4=6(m2),
×3×4=6(m2),
在△ACD中,
∵AD=12m,AC=5m,CD=13m,
∴AD2+AC2=CD2,
∴△ACD是直角三角形,
∴S△ACD= ![]() ×5×12=30(m2).
×5×12=30(m2).
∴四边形ABCD的面积=S△ABC+S△ACD=6+30=36(m2).
【解析】抓住已知条件∠B=90°,因此连接AC,构造直角三角形,将要所求的问题转化到直角三角形中求解。利用勾股定理及逆定理即可求得这块草地的面积。
【考点精析】关于本题考查的勾股定理的概念和勾股定理的逆定理,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形才能得出正确答案.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目