题目内容
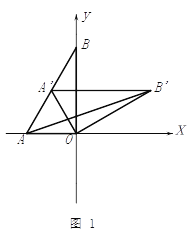
【题目】如图1,在平面直角坐标系, ![]() 为坐标原点,点
为坐标原点,点![]() ,点
,点![]() .
.
(1)求![]() 的度数;
的度数;
(2)如图1,将⊿![]() 绕点
绕点![]() 顺时针得⊿
顺时针得⊿![]() ,当
,当![]() 恰好落在
恰好落在![]() 边上时,设⊿
边上时,设⊿![]() 的面积为
的面积为![]() ,⊿
,⊿![]() 的面积为
的面积为![]() ,
,![]() 与
与![]() 有何关系?为什么?
有何关系?为什么?
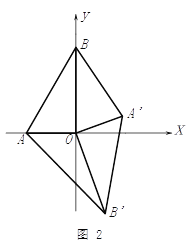
(3)若将⊿![]() 绕点
绕点![]() 顺时针旋转到如图2所示的位置,
顺时针旋转到如图2所示的位置, ![]() 与
与![]() 的关系发生变化了吗?证明你的判断.
的关系发生变化了吗?证明你的判断.
【答案】(1)![]() ;
;
(2)![]() ,理由见解析;
,理由见解析;
(3)![]() 与
与![]() 的关系没变,即
的关系没变,即![]() ,理由见解析.
,理由见解析.
【解析】试题分析:本题的⑴问求![]() 的度数化归在
的度数化归在![]() △
△![]() 来解决,根据点
来解决,根据点![]() ,点
,点![]() 容易求出
容易求出![]() 的长度,利用三角函数的定义计算出三角函数值,从而求出该角的度数.
的长度,利用三角函数的定义计算出三角函数值,从而求出该角的度数.
本题的⑵问抓住⊿![]() 和⊿
和⊿![]() 的边
的边![]() 是同一三角形⊿
是同一三角形⊿![]() 的边;根据旋转的特征可以推出
的边;根据旋转的特征可以推出![]() ,结合⑴问容易推出三角形⊿
,结合⑴问容易推出三角形⊿![]() 是等边三角形,等边三角形不但三边相等,而且三边上的高也是相等的,我们利用“等底等高的三角形”的结论容易判断出
是等边三角形,等边三角形不但三边相等,而且三边上的高也是相等的,我们利用“等底等高的三角形”的结论容易判断出![]() .
.
本题的⑶问也抓住根据旋转的特征可以推出⊿![]() 和⊿
和⊿![]() 的边
的边![]() ;其实我们只需找到
;其实我们只需找到![]() 边上高相等;而
边上高相等;而![]() 边上的高可以化在两个三角形中,通过全等三角形可以证得其高相等,再利用“等底等高的三角形”的结论容易判断出
边上的高可以化在两个三角形中,通过全等三角形可以证得其高相等,再利用“等底等高的三角形”的结论容易判断出![]() .(本问也可以用相似形的相关知识使问题获得解决.)
.(本问也可以用相似形的相关知识使问题获得解决.)
试题解析:(1)∵点![]() ,点
,点![]()
∴![]()
又![]()
∴![]()
∴![]()
(2)![]() .
.
理由如下:

根据旋转的征可知: ![]() .又
.又![]()
∴⊿![]() 是等边三角形
是等边三角形
∴![]()
∴![]() ∥
∥![]() 轴
轴
∴点![]() 到
到![]() 轴的距离相等(图中
轴的距离相等(图中![]() )
)
∵等边⊿![]() 的三条高都相等(图中
的三条高都相等(图中![]() )
)
∴点![]() 到
到![]() 的距离等于点
的距离等于点![]() 到
到![]() 轴的距离(图中
轴的距离(图中![]() )
)
∴![]() (等底等高的三角形面积相等)
(等底等高的三角形面积相等)
(3)![]() 与
与![]() 的关系没变,即
的关系没变,即![]() .
.
理由如下:
过点作![]() 于
于![]() ,过点
,过点![]() 作
作![]()
![]() 于
于![]() .
.

∴![]()
根据题意可知: ![]()
根据旋转的征可知: ![]()
∴![]()
∴![]()
∴⊿![]() ≌⊿
≌⊿![]() (
(![]() )
)
∴![]()
又∵![]()
∴![]() (等底等高的三角形面积相等)
(等底等高的三角形面积相等)

 新课标阶梯阅读训练系列答案
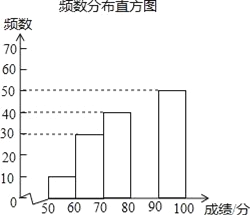
新课标阶梯阅读训练系列答案【题目】中华文明,源远流长;中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | n |
80≤x<90 | m | 0.35 |
90≤x≤100 | 50 | 0.25 |
请根据所给信息,解答下列问题:
(1)m= ,n= ;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在 分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?